Problem G. 861. (October 2024)

G. 861. Anna took her dog Buddy for a walk. Anna was walking on the avenue at a speed of \(\displaystyle 0.8~\mathrm{m}/\mathrm{s}\) when she dropped her house key near a linden tree. At this instant Buddy was at the litter bin, 4 m away from the linden tree, and he was trotting at a speed of \(\displaystyle 1.2~\mathrm{m}/\mathrm{s}\). When Buddy reached the lamppost, \(\displaystyle 3.6\) m away from the litter bin, he turned back and began to trot back and forth between the litter bin and the lamppost at the same constant speed of \(\displaystyle 1.2~\mathrm{m}/\mathrm{s}\). When Anna reached the litter bin, she noticed that she had dropped the key, so she turned back to get it. She was moving at \(\displaystyle 0.8~\mathrm{m}/\mathrm{s}\) the whole time. How did the length of the retractable leash, which was kept taut, change from the time she dropped the key to the time she picked it up? Plot a graph.

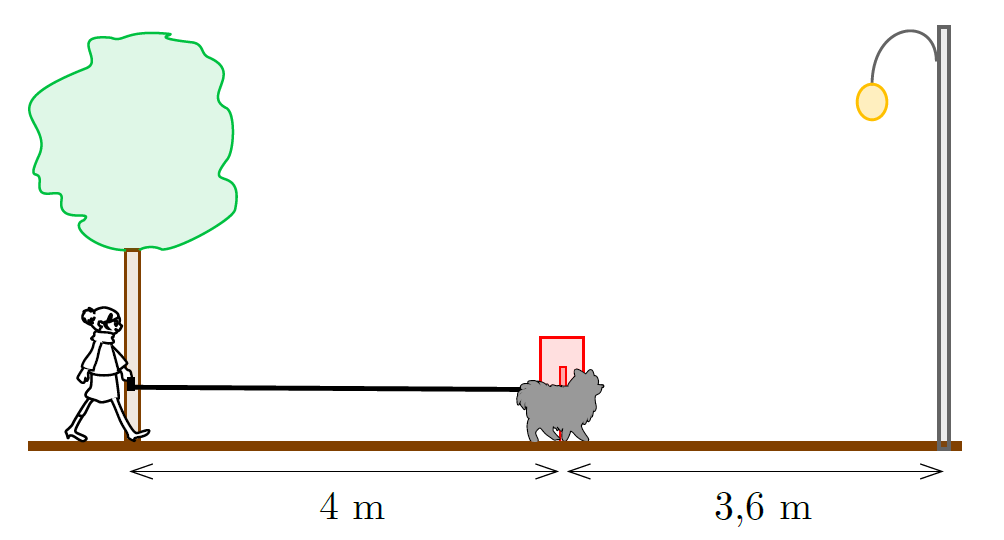
(4 pont)

Deadline expired on November 15, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az 1. ábrán Panni (piros vonal) és Fickó (kék vonal) elmozdulás-idő grafikonját ábrázoltuk. Az \(\displaystyle x\) tengely origója a hársfánál van, az időt pedig attól kezdve mérjük, hogy Panni elhalad a fa mellett. Panni \(\displaystyle 5\,\mathrm{s}\) alatt teszi meg a fa és a szemeteskuka közötti távolságot, Fickó pedig \(\displaystyle 3\,\mathrm{s}\) alatt ér a szemeteskukától a lámpáig.

1. ábra

A póráz hossza minden pillanatban a két helyzet különbsége. Amikor mindketten egyenletes sebességgel mozognak, akkor a kötél hossza is egyenletesen változik, így csak azokban a pontokban kell számolnunk, ahol valamelyik grafikonnak töréspontja van. Ezekben az időpontokban Fickó és Panni helyzetét, valamint a póráz \(\displaystyle d\) hosszát az alábbi táblázatban foglaltuk össze.

A táblázat alapján már könnyen megrajzolhatjuk a 2. ábrát, melyen a póráz hossza látható az idő függvényében.

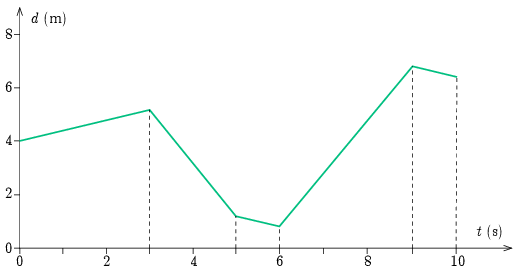
2. ábra

Statistics:

49 students sent a solution.
4 points:	Békési Máté, Blaskovics Bálint, Dombóvári Nándor, Hegedüs Márk, Horváth Zsombor, Huba Zsombor , Kakas Noel, Kámán-Gausz Péter, Kis Dániel, Klenkó Éva Borbála, Kossár Benedek Balázs, Kovács Artúr-Lehel, Kovács Tamás , Medgyesi András, Németh Ábel, Palik Csenge, Patócs 420 Péter, Sipos Dániel Sándor, Szabó András, Szighardt Anna, Szűcs Kitti, Tóth Domonkos, Zsuga Medárd.
3 points:	Csonka Áron, Lakatos Levente, Majer Veronika, Sógor-Jász Soma, Vincze Blanka Anna, Vízhányó Janka.
2 points:	8 students.
1 point:	4 students.
Not shown because of missing birth date or parental permission:	5 solutions.

Problems in Physics of KöMaL, October 2024