A G. 862. feladat (2024. október)

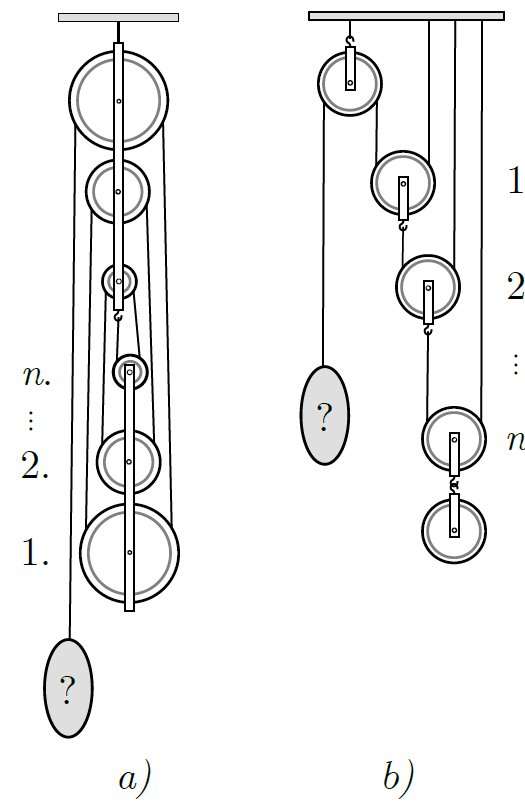
G. 862. Egy csigasor $\displaystyle n$ darab, a méretétől függetlenül $\displaystyle G$ súlyú mozgócsigából áll, a kötél ideálisnak tekinthető. Mekkora súlyt akasszunk a kötél végére, hogy a rendszer egyensúlyban legyen, ha a csigasor

$\displaystyle a)$ lineáris és terheletlen ($\displaystyle a)$ ábra),

$\displaystyle b)$ arkhimédészi, és egy $\displaystyle G$ súlyú csigával terheljük ($\displaystyle b)$ ábra)?

(4 pont)

A beküldési határidő 2024. november 15-én LEJÁRT.

Megoldás. a) Az $\displaystyle n$ mozgócsigát összesen $\displaystyle 2n$ kötél tartja (mindegyik mozgócsiga jobb és bal oldalán egy-egy kötél). A kötélben végig azonos a feszítettség, tehát az $\displaystyle n$ mozgócsiga $\displaystyle nG$ súlyával $\displaystyle 2nF$ erő tart egyensúlyt ($\displaystyle 2nF=nG$). Így a rendszer egyensúlyához $\displaystyle F=G/2$ súlyú testet kell a kötél végére akasztani.

b) Az utolsó mozgócsiga a ráakasztott terheléssel együtt $\displaystyle 2G$ súlyú, vagyis az utolsó mozgócsiga jobb és bal oldalához tartozó két kötélszárban a feszítőerő ennek fele, tehát $\displaystyle G$. Az utolsó előtti mozgócsiga $\displaystyle G$ súlyához a kötél még ugyanekkora $\displaystyle G$ erővel járul hozzá, így az ehhez a csigához tartozó két kötélszárban szintén $\displaystyle G$ a feszítőerő. Ugyanezt a megfontolást tehetjük rendre az összes mozgócsigára, tehát az egyes (egymástól független) kötéldarabokban mindenhol $\displaystyle G$ a feszítőerő, vagyis az állócsigán átvetett kötél végére egy $\displaystyle G$ súlyú testet kell akasztanunk.

Statisztika:

32 dolgozat érkezett.
4 pontot kapott:	Békési Máté, Csáki Anikó, Csonka Áron, Hegedüs Márk, Horváth Zsombor, József Áron, Kovács Artúr-Lehel, Majer Veronika, Patócs 420 Péter, Sipeki Andor, Szabó András, Szighardt Anna, Szilaj Petra, Szűcs Kitti, Tóth Domonkos.
3 pontot kapott:	Vízhányó Janka.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2024. októberi fizika feladatai