 Problem G. 882. (March 2025)
Problem G. 882. (March 2025)
G. 882. The system shown in the figure is in equilibrium, the rope in the middle is horizontal.
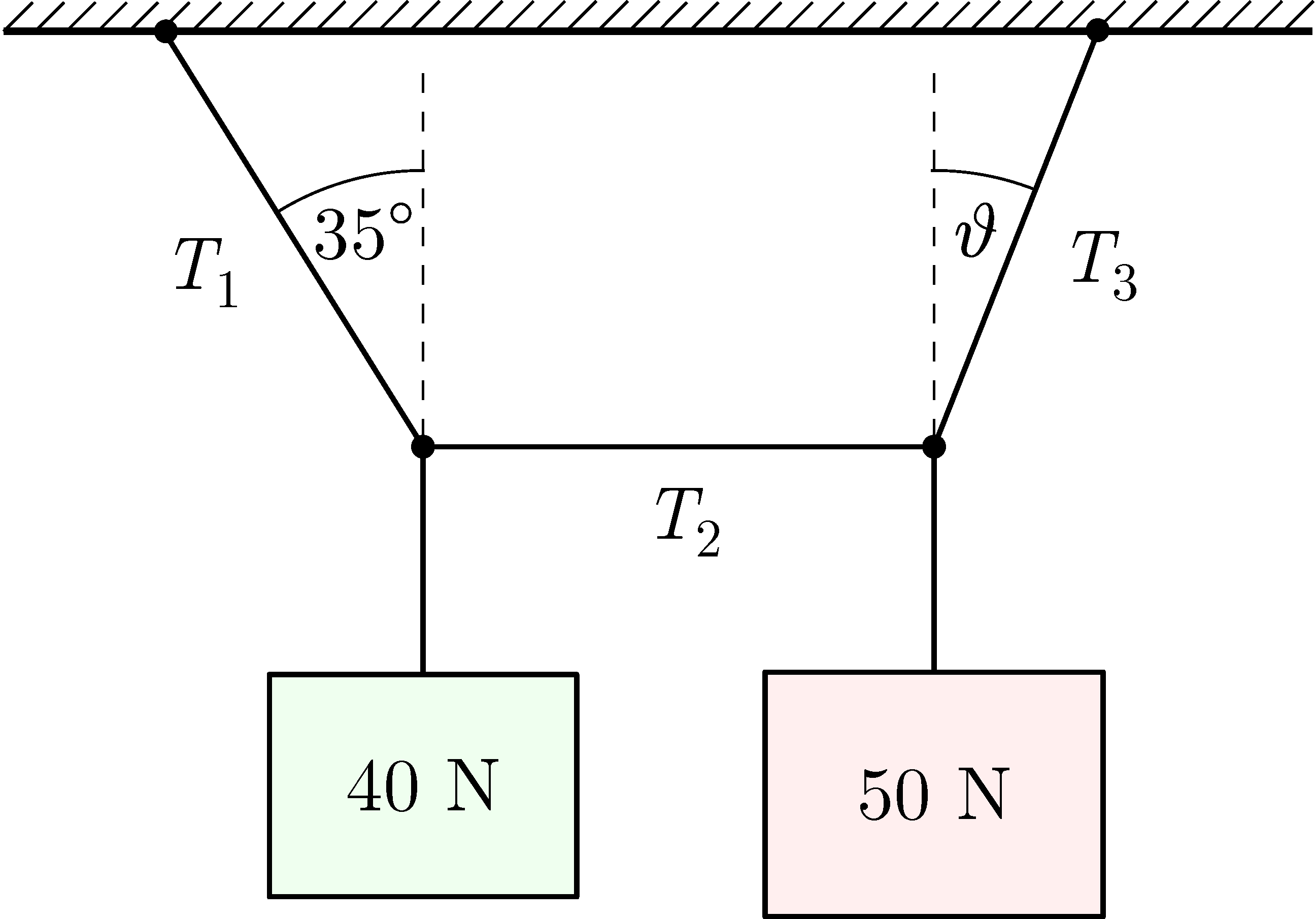
a) On graph paper construct the forces with a ruler and a protractor to determine the tension exerted in the ropes and the value of the unknown angle \(\displaystyle \vartheta\).
b) Estimate the percentage error of the constructed quantities.
(4 pont)
Deadline expired on April 15, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. a) A kényelem kedvéért a milliméterpapíron a skálát úgy válasszuk meg, hogy 1 N erő 1 mm-t jelentsen. A szerkesztést az alábbi ábra mutatja:
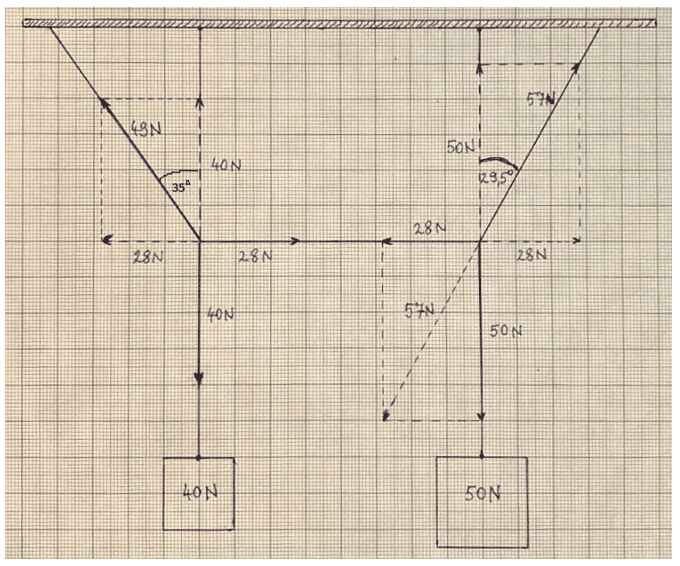
A tartóköteleknek két csomópontja van, azokba három-három kötélszár fut be, az ezekhez tartozó kötélerők az egyes csomópontokban kiegyensúlyozzák egymást. A szerkesztést a bal oldali csomóponttal kezdjük.
A 40 N-os erő függőleges, ezzel \(\displaystyle 35^\circ\)-os szöget zár be a \(\displaystyle T_1\) erő, illetve a \(\displaystyle T_2\) erő vízszintes. A szöget felmérve, majd a 40 N-os erő ellentettjét berajzolva, végül párhuzamosok berajzolásával leolvashatjuk, hogy \(\displaystyle T_1=49\,\mathrm{N}\) és \(\displaystyle T_2=28\,\mathrm{N}\).
A \(\displaystyle T_2=28\,\mathrm{N}\)-os erőt másoljuk át a jobb oldali csomópontba, és vegyük fel a függőleges irányú 50 N-os nehézségi erőt is. Ezek összege adja a \(\displaystyle T_3\) erő ellentettjét. A rajzról leolvashatjuk, hogy \(\displaystyle T_3=57\,\mathrm{N}\), illetve \(\displaystyle \vartheta=29{,}5^\circ\).
b) Durván azt mondhatjuk, hogy \(\displaystyle 0{,}5\,\mathrm{mm}\)-es pontossággal tudjuk az erőket leolvasni, ami 1%-os hibát jelent a nagyobb erők, illetve 2%-os hibát a kisebb erő esetében. A szöget fél fok pontossággal olvashatjuk le, ami a jelen esetben 2%-nál valamivel kisebb hibát jelent.
Megjegyzés. Szögfüggvények, illetve Pitagorasz-tétel segítségével is megkaphatjuk a kérdéses adatokat:
$$\begin{gather*} T_1=\frac{40\,\mathrm{N}}{\cos{35^{\circ}}}=48{,}83\,\mathrm{N}\qquad\Rightarrow\qquad\frac{\Delta T_1}{T_1}=3{,}5\cdot 10^{-3}=0{,}35\%,\\ T_2=40\,\mathrm{N}\cdot\tg{35^{\circ}}=28{,}01\,\mathrm{N}\qquad\Rightarrow\qquad\frac{\Delta T_2}{T_2}=3\cdot 10^{-4}=0{,}03\%,\\ T_3=\sqrt{T_2^2+(50\,\mathrm{N})^2}=57{,}31\,\mathrm{N}\qquad\Rightarrow\qquad\frac{\Delta T_3}{T_3}=5{,}4\cdot 10^{-3}=0{,}54\%,\\ \sin{\vartheta}=\frac{T_2}{T_3}=0{,}4887\qquad\Rightarrow\qquad\vartheta=29{,}26\,^\circ\qquad\Rightarrow\qquad\frac{\Delta\vartheta}{\vartheta}=8{,}3\cdot 10^{-3}=0{,}83\%. \end{gather*}$$Láthatjuk, hogy gondos szerkesztéssel a durva becsléssel megállapított hibahatárnál pontosabb eredményeket kaphatunk.
Statistics:
26 students sent a solution. 4 points: Békési Máté, Csáki Anikó, Hegedüs Márk, Hollósi Dominik, Horváth Zsombor, Kossár Benedek Balázs, Kovács Artúr-Lehel, Lakatos Levente, Molnár Sámuel , Sipeki Andor, Sógor-Jász Soma, Szabó András, Szighardt Anna, Vincze Blanka Anna, Vízhányó Janka. 3 points: Csonka Áron, Kovács Tamás , Németh Ábel. 2 points: 3 students. 1 point: 1 student. 0 point: 1 student.
Problems in Physics of KöMaL, March 2025
