Problem G. 885. (April 2025)

G. 885. The refractive index of the core of an optical fibre is 1.6 and that of the cladding is 1.5. What can the maximum angle between a ray of light and the axis of the optical fibre be in order to produce total reflection inside the fibre? A light ray enters from air into the glass fibre at the centre of the cross sectional plane of the fibre, which is perpendicular to the symmetry axis of the fibre. What is the maximum angle of incidence of the light ray?

(3 pont)

Deadline expired on May 15, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Teljes visszaverődés az üvegszál magja (angolul core) és borítása (angolul cladding) között jön létre, ahogy ezt az ábra mutatja.

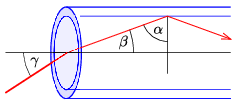
Az \(\displaystyle \alpha\) szög legyen a teljes visszaverődés határszöge, amit így számíthatunk ki:

\(\displaystyle \sin\alpha=\frac{n_2}{n_1}=\frac{1{,}5}{1{,}6}\qquad\Rightarrow\qquad\alpha=69{,}6^\circ\approx 70^\circ,\)

ahol \(\displaystyle n_1\) az üvegszál magjának, \(\displaystyle n_2\) pedig a borításának a törésmutatója. Mivel \(\displaystyle \beta\) éppen \(\displaystyle \alpha\) pótszöge (a derékszögű háromszög két hegyesszögének összege alapján), a fénysugár legfeljebb \(\displaystyle \beta=20^\circ\)-os szöget zárhat be az üvegszál tengelyével.

A \(\displaystyle \gamma\) szöget a Snellius–Descartes-törvény alapján számíthatjuk ki:

\(\displaystyle \frac{\sin\gamma}{\sin\beta}=n_1=1{,}6\qquad\Rightarrow\qquad\gamma=33^\circ.\)

Tehát a tengelyhez képest legfeljebb \(\displaystyle 33^\circ\)-os szöget bezáróan érkezhet a fénysugár az üvegszál belépő lapjának közepére.

Statistics:

23 students sent a solution.
3 points:	Békési Máté, Hegedüs Márk, Horváth Zsombor, József Áron, Kovács Artúr-Lehel, Macskássy Márk, Majer Veronika, Medgyesi András, Molnár Sámuel , Sógor-Jász Soma, Szilaj Petra, Tóth Domonkos, Vízhányó Janka.
2 points:	Bora Ádám, Csáki Anikó, Hollósi Dominik, Kovács Tamás , Rácz Koppány Bendeguz.
1 point:	1 student.
0 point:	1 student.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Physics of KöMaL, April 2025