Problem G. 886. (April 2025)

G. 886. Two identical parallel plate capacitors are connected in parallel, as shown in the figure. They are charged to 200 V and then the voltage source is disconnected. Then the distance between the plates of one of the capacitors is doubled and that of the other is halved. (There's air between the plates.)

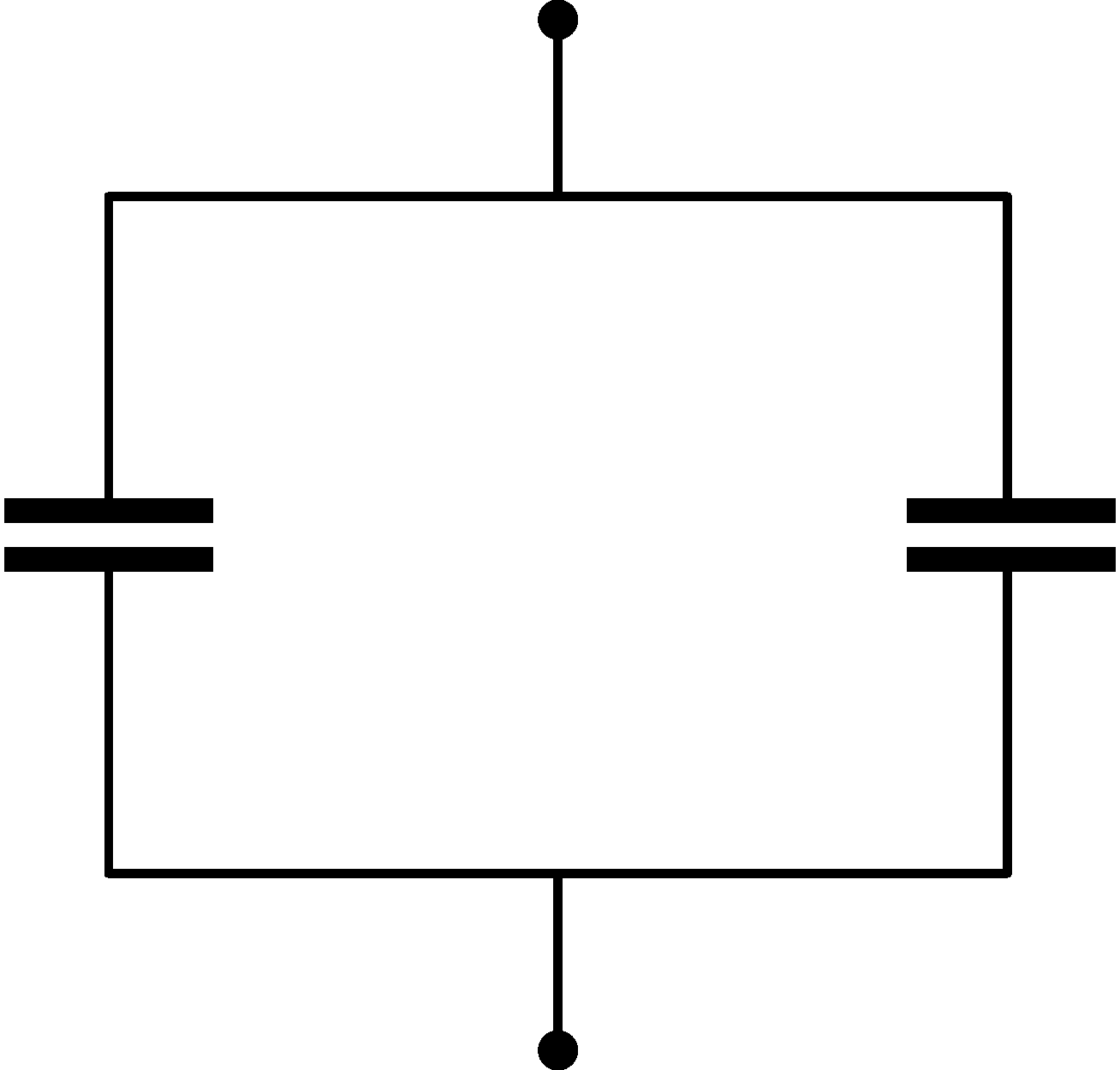
a) By what factor does the equivalent capacitance of the system change?

b) What will the voltage be?

c) By what percentage does the energy stored in each capacitor change?

(4 pont)

Deadline expired on May 15, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. (ÍRTA: HGy) a) Legyen mindkét kondenzátor kapacitása kezdetben \(\displaystyle C\). Mivel a két kondenzátor párhuzamosan van kapcsolva, ezért kezdetben az eredő kapacitás \(\displaystyle C_\mathrm{e}=2C\). A síkkondenzátorokról tudjuk, hogy kapacitásuk így írható fel:

\(\displaystyle C=\varepsilon_0\frac{A}{d},\)

ahol \(\displaystyle A\) a lemezek felülete, \(\displaystyle d\) a közöttük lévő távolság, \(\displaystyle \varepsilon_0\) pedig a vákuum dielektromos állandója. Ha tehát megkétszerezzük a lemezek közötti távolságot, akkor a kondenzátor kapacitása fele akkora lesz: \(\displaystyle \tfrac{C}{2}\). Ha viszont megfelezzük a lemeztávolságot, akkor a kapacitás kétszeresére nő: \(\displaystyle 2C\). Így végül egy \(\displaystyle 2C\) és egy \(\displaystyle \tfrac{C}{2}\) kapacitású kondenzátort kapcsolunk párhuzamosan, így az új eredő kapacitás \(\displaystyle C_\mathrm{e}'=\tfrac{5}{2}C\)-nek adódik. Tehát a kezdeti eredő kapacitás \(\displaystyle \tfrac{5}{4}=1{,}25\)-szörösére növekszik.

b) Kezdetben mindkét kondenzátor feszültsége \(\displaystyle U=200\,\mathrm{V}\), töltésük pedig külön-külön \(\displaystyle Q=CU\) volt. A megoldás kulcsa az, hogy a kezdeti \(\displaystyle 2Q\) töltés megmarad, az egyik kondenzátornak (\(\displaystyle Q+q\))-ra nő a töltése, a másiké (\(\displaystyle Q-q\))-ra csökken. A párhuzamos kapcsolás miatt a két kondenzátor feszültsége megegyezik:

\(\displaystyle U'=\frac{Q+q}{2C}=\frac{Q-q}{C/2} \qquad\Rightarrow\qquad q=\frac{3}{5}Q \qquad\Rightarrow\qquad U'=\frac{Q+\frac{3}{5}Q}{2C}\left(=\frac{Q-\frac{3}{5}Q}{C/2}\right)=\frac{4}{5}\frac{Q}{C}=\frac{4}{5} U=160\,\mathrm{V}.\)

Az eredményt az a) rész eredményéből is megkaphatjuk, hiszen a feszültség az össztöltés és az eredő kapacitás hányadosa:

\(\displaystyle U'=\frac{2Q}{C_\mathrm{e}'}=\frac{4}{5}U=160\,\mathrm{V}.\)

c) Mindkét kondenzátor kezdeti energiája \(\displaystyle \tfrac{1}{2}QU\) alakban írható fel. Az egyik kondenzátor töltése \(\displaystyle \tfrac{8}{5}Q\)-ra növekszik, a másiké \(\displaystyle \tfrac{2}{5}Q\)-ra csökken, míg mindkettő feszültsége \(\displaystyle U'=\tfrac{4}{5}U\)-ra csökken. Így az egyik energiája \(\displaystyle \tfrac{1}{2}\left(\tfrac{8}{5}Q\cdot\tfrac{4}{5}U\right)=\tfrac{16}{25}QU\)-ra növekszik, ami 28%-os növekedés. A másik energiája \(\displaystyle \tfrac{1}{2}\left(\tfrac{2}{5}Q\cdot \tfrac{4}{5}U\right)=\tfrac{4}{25}QU\)-ra csökken, ami 68%-os csökkenés.

Megjegyzés. A teljes rendszer energiája \(\displaystyle QU\)-ról \(\displaystyle \tfrac{16}{25}QU+\tfrac{4}{25}QU=\tfrac{4}{5}QU\)-ra csökken, ami 20%-os csökkenés. Ez egyezésben van azzal, hogy a rendszer össztöltése nem változik, de a feszültsége 20%-kal csökken.

Statistics:

30 students sent a solution.
4 points:	Békési Máté, Csáki Anikó, Hegedüs Márk, Hollósi Dominik, Horváth Zsombor, József Áron, Kakas Noel, Kovács Artúr-Lehel, Kovács Tamás , Lakatos Levente, Majer Veronika, Medgyesi András, Németh Ábel, Patócs 420 Péter, Rácz Koppány Bendeguz, Sipeki Andor, Sógor-Jász Soma, Szighardt Anna, Szilaj Petra, Tóth Domonkos, Vízhányó Janka.
3 points:	Csonka Áron, Kossár Benedek Balázs, Molnár Sámuel .
2 points:	1 student.
1 point:	1 student.

Problems in Physics of KöMaL, April 2025