Problem G. 888. (April 2025)

G. 888. In an amusement park inside a giant rotating cylinder, people cling to a slant surface attached to the cylinder's mantle. The radius of the cylinder is \(\displaystyle R=5\,\mathrm{m}\), the coefficient of static friction is \(\displaystyle \mu=0.25\), and the slant surface makes an angle of \(\displaystyle \vartheta=30^{\circ}\) with the vertical as shown in the figure.

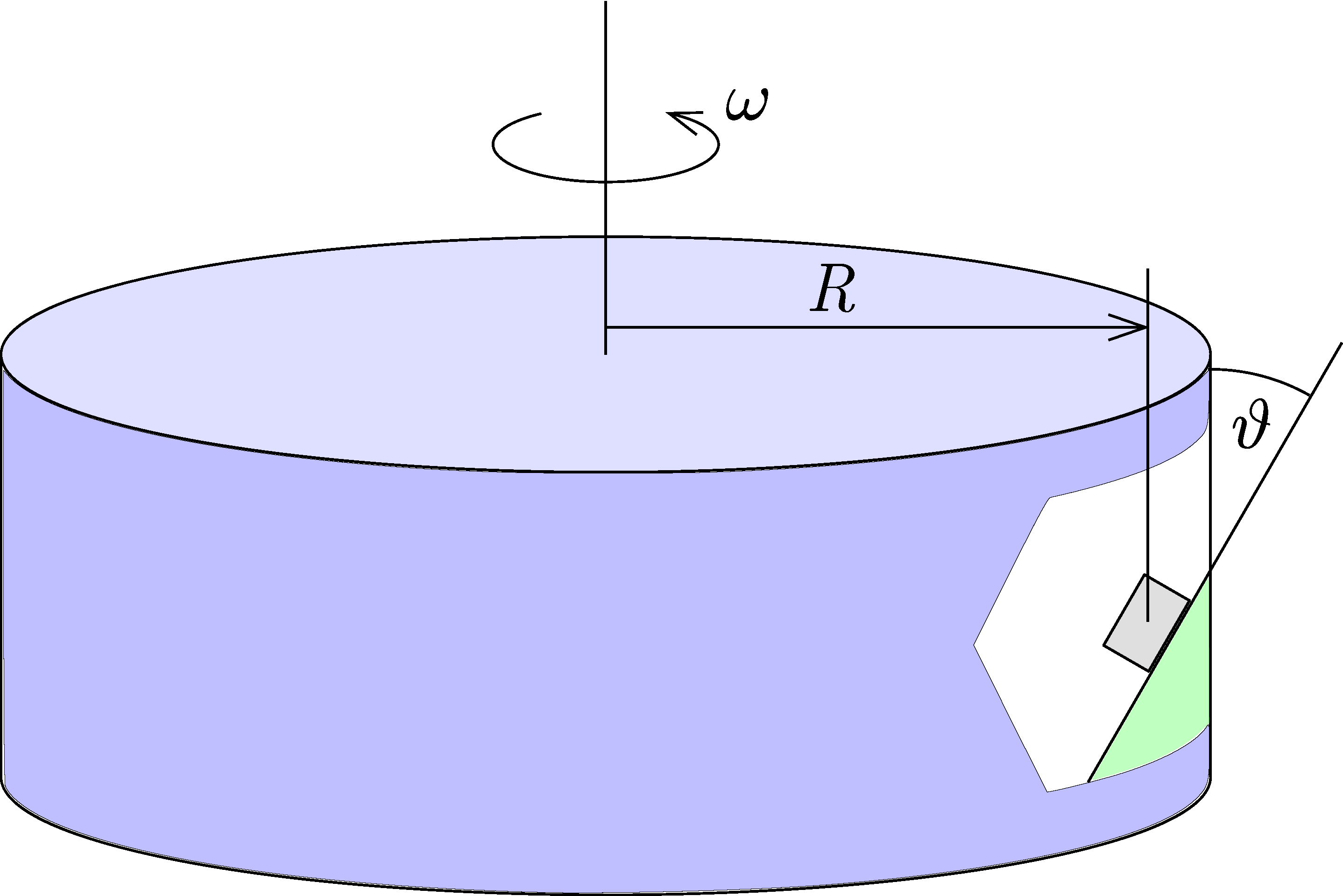
a) What is the minimum and maximum angular speed of the cylinder so that people do not slide up or down?

b) What is the coefficient of friction such that people do not slip off at any small angular velocity?

c) What is the coefficient of friction such that people do not slide upwards at any angular velocity?

(4 pont)

Deadline expired on May 15, 2025.

Sorry, the solution is available only in Hungarian. Google translation

I. megoldás. a) A hengerrel együtt mozgó rendszerben a ferde felületen lévő testek egyensúlyi állapotban nyugszanak, a rájuk ható erők eredője nulla: \(\displaystyle m\boldsymbol{g}+\boldsymbol{N}+\boldsymbol{S}+\boldsymbol{F}_\mathrm{cf}=0\). Az 1. ábra mutatja az \(\displaystyle mg\) nehézségi erőt, a ferde sík által kifejtett \(\displaystyle N\) nyomóerőt, az \(\displaystyle S=\pm\mu N\) súrlódási erőt és az \(\displaystyle F_\mathrm{cf}=mR\omega^2\) centrifugális erőt. A súrlódási erőben megjelenő \(\displaystyle \pm\) jel arra utal, hogy a számításban a két határesetet tekintjük; a + jelnek az felel meg, amikor a súrlódás még éppen meg tudja akadályozni a test lecsúszását, míg a \(\displaystyle -\) jel esetében a felfelé történő megcsúszást képes még megakadályozni.

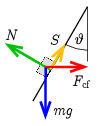
1. ábra

Tekintsük rendre a lejtővel párhuzamos és a lejtőre merőleges összetevők egyensúlyát:

\(\displaystyle mg\cos\vartheta=\pm\mu N+mR\omega^2\sin\vartheta,\)

\(\displaystyle N=mR\omega^2\cos\vartheta+mg\sin\vartheta.\)

A kérdéses szögsebességeket megkapjuk, ha a második egyenletből \(\displaystyle N\)-et beírjuk az elsőbe:

\(\displaystyle \omega=\sqrt{\frac{g(\cos\vartheta\mp\mu\sin\vartheta)}{R(\sin\vartheta\pm\mu\cos\vartheta)}}.\)

Behelyettesítés után azt kapjuk, hogy \(\displaystyle \omega_\mathrm{min}=1{,}42\,\mathrm{s}^{-1}\) (ekkor a számlálóban a \(\displaystyle -\) előjelet, a nevezőben a \(\displaystyle +\) előjelet használtuk), illetve \(\displaystyle \omega_\mathrm{max}=2,62\,\mathrm{s}^{-1}\) (fordított előjelhasználattal).

b) Ha a henger áll, akkor \(\displaystyle \omega=0\), ami azt jelenti, hogy az emberek akkor nem csúsznak le. ha olyan nagy a súrlódás, hogy \(\displaystyle \mu>\frac{1}{\tg\vartheta}=1{,}73.\) (Vigyázat! A függőlegestől mérjük a \(\displaystyle \vartheta\) szöget.)

c) A szögsebesség kifejezésében a nevező nem lehet nulla, sőt negatív sem lehet. Ha formálisan ez jön ki, vagyis \(\displaystyle \mu\geq\tg\vartheta =0{,}577\), akkor a test annyira ráfeszül a ferde síkra, hogy akármilyen nagy \(\displaystyle \omega\) esetén sem csúszik felfelé.

II. megoldás. Egy test akkor nem csúszik meg, ha a nyomóerő és a tapadó súrlódási erő eredője egyensúlyt tud tartani a testre ható többi erő eredőjével. Mivel \(\displaystyle S\leq\mu N\), a két erő eredője legfeljebb

\(\displaystyle \varepsilon=\arctg\frac{S_\mathrm{max}}{N}=\arctg\mu\)

szöget zárhat be a felület normálisával (a felületre merőleges iránnyal). Esetünkben a testre a nyomóerőn és a súrlódási erőn kívül csak a nehézségi erő és a forgó rendszerben fellépő centrifugális erő hat. Mindkét erő arányos a test tömegével, így a két erő eredőjének irányát a függőlegesen lefelé mutató \(\displaystyle g\) és a vízszintesen, sugárirányban kifelé mutató \(\displaystyle a_\mathrm{cf}=\omega^2R\) gyorsulásvektorok \(\displaystyle a\) eredőjének iránya határozza meg.

A feladatunk esetében ez azt jelenti, hogy a két gyorsulásvektor eredője a vízszintessel \(\displaystyle \vartheta-\varepsilon\leq\alpha\leq\vartheta+\varepsilon\) szöget zárhat be (2. ábra).

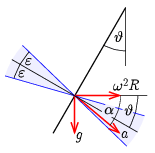
2. ábra

Az ábráról az is látszik, hogy \(\displaystyle \ctg\alpha=\omega^2\tfrac{R}{g}\). Ezután az egyes kérdésekre a válaszok:

a) A súrlódási együttható \(\displaystyle \mu=0{,}25\), ebből \(\displaystyle \varepsilon=\arctg\mu\approx 14^\circ\), \(\displaystyle \vartheta-\varepsilon\approx 16^\circ\), \(\displaystyle \vartheta+\varepsilon\approx 44^\circ\). A szögsebesség-tartományt keressük:

\(\displaystyle \omega=\sqrt{\frac{g}{R}\ctg\alpha},\)

ahol \(\displaystyle \vartheta-\varepsilon\leq\alpha\leq\vartheta+\varepsilon\). A minimális szögsebességhez a maximális \(\displaystyle \alpha\) szög tartozik (és fordítva), így:

b) \(\displaystyle \omega=0\) esetében az eredő gyorsulás függőleges (csak a nehézségi erő hat), így teljesülnie kell a \(\displaystyle \vartheta+\varepsilon\geq 90^\circ\) egyenlőtlenségnek. Ebből \(\displaystyle \varepsilon\geq 60^\circ\) és így \(\displaystyle \mu\geq\tg 60^\circ\approx 1{,}73\) szükséges.

c) Nagyon nagy szögsebesség esetében az eredő gyorsulás közel vízszintes, így a \(\displaystyle \varepsilon\geq\vartheta\) egyenlőtlenségnek kell teljesülnie, amiből \(\displaystyle \varepsilon\geq 30^\circ\) és így \(\displaystyle \mu\geq\tg 30^\circ\approx 0{,}57\) szükséges.

Statistics:

26 students sent a solution.
4 points:	Békési Máté, Csáki Anikó, Hegedüs Márk, Horváth Zsombor, Kossár Benedek Balázs, Kovács Tamás , Lakatos Levente, Macskássy Márk, Molnár Sámuel , Németh Ábel, Patócs 420 Péter, Rácz Koppány Bendeguz, Sipeki Andor, Sógor-Jász Soma, Szabó Tamás.
3 points:	Csonka Áron, Vízhányó Janka.
2 points:	3 students.
1 point:	1 student.
0 point:	1 student.

Problems in Physics of KöMaL, April 2025