Az I/S. 16. feladat (2017. március)

I/S. 16. Zénó szereti a betűrejtvényeket és mániákusan gyűjti az értelmes és értelmetlen szavakat. Egy-egy táblázat soraiban gyűjti az azonos hosszúságú karaktersorozatokat, amelyek valahol valamilyen rejtvényben már felbukkantak, minden cellába egy-egy betűt írva. A táblázatra igaz, hogy az egy-egy oszlopban levő karakterekből álló szavak különbözőek.

Miki, a barátja meg akarja tréfálni Zénót. A táblázat tetejéről a lehető legtöbb sort akarja törölni úgy, hogy Zénó ne vegye észre, azaz a ,,nincs két azonos oszlop'' szabály igaz maradjon. Segíts Mikinek programot írni, amely meghatározza, hány sort töröljön.

A standard bemenet első sora a táblázat sorainak és oszlopainak a számát \(\displaystyle S\), \(\displaystyle O\) (\(\displaystyle 1 \le S,O \le 1000\)) tartalmazza. A következő \(\displaystyle S\) sor \(\displaystyle O\) darab kisbetűs, az angol ábécé karaktereiből álló szót tartalmaz, Zénó táblázatának szavait, a leírt sorrendben. A táblázatra igaz, hogy nincs benne két azonos oszlop.

A standard kimenet egyetlen sorába írjuk azt a legnagyobb számot, ahány sort Miki törölhet a táblázat elejéről úgy, hogy bármely két oszlop különböző maradjon.

Példák:

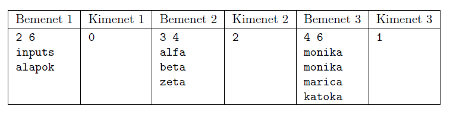
Időlimit: 1 mp, memórialimit: 256 MB.

Figyelem! A bemenet mérete nagy, így a főprogram nem futhat egy egész másodpercig.

Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a fenti korlátoknak megfelelően.

Beküldendő egy tömörített is16.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2017. április 10-én LEJÁRT.

Ha \(\displaystyle K\) sort tudunk törölni a mátrix tetejéről úgy, hogy ne maradjon két egyforma oszlop, akkor \(\displaystyle K-1\) sor törlésével is teljesül ez a feltétel. Emiatt a tulajdonság miatt a maximális \(\displaystyle K\) bináris kereséssel található meg.

Hatékony eljárást kell találni, amivel megállapíthatjuk adott \(\displaystyle K\)-ra, hogy az első \(\displaystyle K\) sor elhagyásával ne maradjon két egyforma oszlop. Ha az oszlopokat alulról felfele \(\displaystyle STRING\)-ként kezeljük, akkor könnyen ábécé szerint növekvő sorba tudjuk őket rendezni. Így bármely két, egyformán kezdődő oszlop egymás mellé kerül, emiatt csak a szomszédos elemeket kell \(\displaystyle K\) hosszúságig ellenőrizni.

Az eljárás hatékonysága \(\displaystyle O(N*log(N))\), ahol \(\displaystyle N=max(R,~C)\).

Másik lehetőség az összehasonlításra valamilyen hash-elő eljárás, amivel két szöveg összehasonlítása egészek összehasonlítására vezethető vissza.

Mintamegoldás: main.cpp

Statisztika:

12 dolgozat érkezett.
10 pontot kapott:	Busa 423 Máté, Gáspár Attila, Janzer Orsolya Lili, Kiss Gergely, Nagy Nándor, Németh 123 Balázs, Noszály Áron, Stomfai Gergely, Szakály Marcell, Vári-Kakas Andor.
9 pontot kapott:	Molnár Bálint.
4 pontot kapott:	1 versenyző.

A KöMaL 2017. márciusi informatika feladatai