 |
Az I/S. 6. feladat (2016. február) |
I/S. 6. Adott N (1≤N≤1000) db tornyunk. Minden toronynak ismerjük a magasságát, ami egész szám 0-tól 100-ig. Akkor tekintjük szépnek a városunkat, ha bármely két torony magasságának különbsége nem nagyobb, mint 17. A város szépítésére építészeket fogadunk. Egy tornyot x emelettel alacsonyabbra átalakítani, vagy x emelettel magasabbra építeni x2 forintba kerül. Adjuk meg, mennyi pénzből tudjuk minimálisan elérni, hogy szép legyen a városunk. Tornyokat csak egész számú emelettel tudunk változtatni. Az átépítés után is teljesülnie kell, hogy minden torony magassága nemnegatív egész.
A program olvassa be a standard input első sorából N-et, majd a következő N sorból az egyes épületek magasságát, és írja a standard output első és egyetlen sorába azt a minimális költséget, amellyel a feladat megoldható.
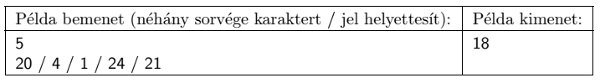
Magyarázat: a 4, 20, 21 magasságú épületeket megtartjuk, az 1-eshez 3-at adunk, a 24-esből 3-at levonunk.
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Beküldendő egy tömörített is6.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
A beküldési határidő 2016. március 10-én LEJÁRT.
Statisztika:
19 dolgozat érkezett. 10 pontot kapott: Bálint Martin, Gergely Patrik, Hornák Bence, Janzer Orsolya Lili, Kiss Gergely, Kovács 246 Benedek, Mernyei Péter, Nagy Ábel, Németh 123 Balázs, Németh 729 Gábor, Noszály Áron, Olexó Gergely, Radnai Bálint, Vári-Kakas Andor. 5 pontot kapott: 1 versenyző. 4 pontot kapott: 1 versenyző. 2 pontot kapott: 3 versenyző.
A KöMaL 2016. februári informatika feladatai
|
|

