 |
Az I. 175. feladat (2008. január) |
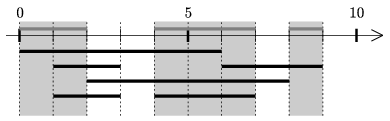
I. 175. Adott a számegyenesen N darab zárt intervallum. Határozzuk meg a számegyenes azon intervallumait, amelyeket az adott intervallumok közül páratlan sok tartalmaz. Az intervallumok végpontjait nem kell vizsgálni. A megoldásban minimális számú intervallum szerepeljen, tehát az intervallumok legyenek diszjunktak, és a szomszédosakat vonjuk össze.
A program az intervallumok leírását fájlból olvassa, az eredményt fájlba írja. A bemeneti, illetve kimeneti fájlok nevei az első, illetve második parancssori argumentumok (például i175 be.txt ki.txt). A bemenet első sora az intervallumok N (0
N7000) számát, az ezt követő N sor mindegyike két szóközzel elválasztott, egész számot, egy-egy intervallum X kezdő- és Y végpontját tartalmazza (). A kimenet első sorában az intervallumok M száma, majd az ezt követő M sorban egy-egy intervallum leírása szerepeljen, a végpontok növekvő sorrendben, a bemenettel megegyező formátumban.
Beküldendő a program forráskódja (i175.pas, i175.cpp, ...), valamint a program rövid dokumentációja (i175.txt, i175.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
A beküldési határidő 2008. február 15-én LEJÁRT.
A megoldás menete
A feladatra nagyon sokféle megoldás érkezett. A következőkben N-nel fogjuk jelölni az intervallumok maximális számát, és L-lel azok maximális hosszát. Feltesszük, hogy minden szám ábrázolható egyetlen gépi szóban.
Tálcán kínálta magát a következő módszer: vegyünk egy L hosszú tömböt, melynek minden eleme azt reprezentálja, hogy az [i,i+1] szakasz felett hány intervallum fut. Kezdetben a tömböt nullázzuk, majd minden intervallumra az összes olyan tömbelem értékét eggyel növeljük, amely felett az adott intervallum átmegy. Ezután a tömbön végigfutva már csak ki kell olvasni azon szakaszait, melyben a értékek paritása páratlan. A módszer kétségkívül helyes megoldást ad, viszont mind tárigénye, mind időigénye nagyon magas. Tárigénye L-nel arányos a tömb miatt, futásideje pedig N.L-lel. (Ha például mind az N intervallum a [0,L], tömbhozzáférés ennyi lesz).
Ennél egy fokkal jobb megoldás, ha változatlanul felvesszük az L hosszú tömböt, de nem a számegyenes egységhosszú szakaszaihoz, hanem az egész számértékekhez. Kezdetben a tömböt itt is nullázzuk, majd minden intervallum feldolgozásakor a kezdőpont indexű tömbelem értékét 1-gyel növeljük, a végponthoz tartozóét pedig eggyel csökkentjük. Miután ezt minden intervallumra megtettük, a tömb minden eleme azt fogja tartalmazni, hogy az adott pontban az intervallumok száma mennyivel változott. A tömb egyszeri végigolvasással ismét könnyen meghatározhatóak a páratlan intervallumok. A módszer tárigénye változatlanul O(L), azonban műveletigénye O(N+L)-re csökkent, hiszen az intervallumok feldolgozása most már csak 2 tömbhozzáférést jelent, függetlenül a hosszuktól, a végeredmény pedig a tömb egyszeri végigolvasásával megkapható.
Egy, még ennél is jobb megoldáshoz az előzőben már megjelent "csak az intervallumok végpontjai számítanak" ötletet kell továbbgondolni: azt kell észrevenni, hogy teljesen mindegy, hogy egy kezdő- vagy végpont melyik intervallumhoz tartozik. Másképp fogalmazva, teljességgel közömbös, hogy egy kezdőpontnak melyik végpont a "párja", a lényeg csupán annyi, hogy egy kezdőpontban az intervallumok száma 1-gyel nő, egy végpontban pedig 1-gyel csökken. Tegyük tehát minden [a,b] intervallum esetén egy tömbbe az (a,1) párt, mely a kezdőpontot, és a (b,-1) párt, mely a végpontot reprezentálja. A párok első tagja tehát azt jelenti, hogy hol, míg utolsó tagja, hogy mennyivel változott az intervallumok száma. A párokat az első tag szerint sorba rendezve, az azonos koordináták szerint csoportosítva, majd a tömböt sorban végigolvasva ismét könnyen adódik a megoldás: azokban a pontokban kezdődik vagy végződik egy páratlan intervallum, melyek szerepelnek a tömbben, és mellettük második tagként a változások összege páratlan. A módszer tárigénye N-nel arányos, míg műveletigénye az alkalmazott rendezési algoritmustól függ, így akár O(N.log (N)) is lehet. Megjegyezzük, hogy igazából a 2. algoritmus is e utolsó módszer egy speciális, ú.n. ládarendezést használó változata.
A megoldások értékelése
A legtöbb versenyző az első módszert választotta, de érkezett egy-egy megoldás a második és harmadikra is. A pontozást illetően figyelembe vettük, hogy az utóbbi két módszer műveletigénye nagyságrendileg kevesebb, ugyanakkor azt is, hogy a feladat szövegében megadott korlátokkal az első módszer szerinti megoldások is lefutottak legfeljebb 1 percen belül (és természetesen utóbbiak a másodperc törtrésze alatt), így hossza vívódás után úgy döntöttünk, hogy az első módszert legfeljebb 9 ponttal jutalmaztuk.
Mintamegoldások
Mintamegoldásként közöljük a hivatalos megoldást C++ nyelven, mely a harmadik módszert implementálja, illetve Fábián András (Szeged, Radnóti Miklós Kísérleti Gimnázium, 11. osztály) versenyző Pascal nyelven írt munkáját (második módszer).
Engedy Balázs
Statisztika:
8 dolgozat érkezett. 10 pontot kapott: Fábián András, Véges Márton. 9 pontot kapott: Adrián Patrik, Földes Imre. 8 pontot kapott: 2 versenyző. 6 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző.
A KöMaL 2008. januári informatika feladatai