Az I. 253. feladat (2010. december)

I. 253. Az alábbi feladatban egy olyan faluvégi utcát vizsgálunk, amelynek csak az egyik oldalán laknak. A helyi szokásoknak megfelelően minden portát festett fakerítés határol, a ház pedig a kerítéstől kicsit bentebb található. Egy-egy porta kerítése egyszínű.

Az utca portáit leíró adatokat az utca.txt állomány tartalmazza. Az állomány sorai az utca portáit valós elhelyezkedésük sorrendjében (az alsó végtől a felső végig) adják meg. A sorok két számot és egy, legfeljebb 20 karakteres szót tartalmaznak. Az első szám a porta utcafront oldali hosszát adja meg méterben (másik kiterjedésükben egyeznek), a másik pedig a kapunak a porta sarkától mért távolságát. (A most pontszerűnek tekintett kapu soha nem kerül telekhatárra.) A szó a kerítés színét adja meg. Az utca hossza legfeljebb 10 km.

Például:

   15 3 sarga
   18 5 kek
   11 4 sarga
   ...

A 2. sor szerint az utca alsó végtől számított második portájának utcahossza 18 méter, a sarkától 5 méterre, az utca elejétől 20 méterre van.

Készítsünk programot, amely az alábbi kérdésekre válaszol. A program forráskódját porta néven mentsük.

A képernyőre írást igénylő részfeladatok eredményének megjelenítése előtt írjuk a képernyőre a feladat sorszámát. Amennyiben a felhasználótól kérünk be adatot, jelenítsük meg a képernyőn, hogy milyen értéket várunk (például 4. feladat: Kérem a lámpaoszlopok távolságát!).

1. Olvassuk be az utca.txt állományban talált adatokat, s annak felhasználásával oldjuk meg a következő feladatokat.

2. Adjuk meg, hány olyan telek van az utcában, amelynek kerítése piros színű.

3. Határozzuk meg, hogy a legnagyobb telek területe hányszorosa a legkisebbnek. Az eredményt két tizedes pontossággal jelenítsük meg.

A faluban most készül a közvilágítás. Az utca kezdetére, a sarokra kerül egy villanyoszlop, majd v méterenként egy-egy újabb. Minden lámpa a kerítésnek ugyanolyan hosszú szakaszát képes megvilágítani, az előtte lévő l métert és az utána levő l métert. v és l egész számok, valamint v2l, azaz a fénykörök legfeljebb érintik egymást.

4. Kérjük be a felhasználótól v és l értékét. A további feladatok megoldásánál ezeket az értékeket használjuk.

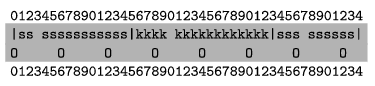
5. Állítsuk elő az utca villanyoszlopokkal kiegészített képét a kep.txt állományban. Az első sorban a kerítések jelenjenek meg, a másodikban a villanyoszlopok. A telekhatárokat a szűrő karakter (|) jelezze, a kaput szóköz. A kerítést színének első karaktere jelölje. A villanyoszlopokat az O betű adja meg. A feladat elején szereplő példának az alábbi képrészlet felel meg 6 méteres oszloptávolság esetén (csak a két szürke hátterű sort kell a kimenetnek tartalmaznia):

6. A világítás sokba kerül, ezért az utca lakói elhatározzák, hogy amíg senki nincs az utcán, csak annyi lámpát tartanak égve, amennyi elegendő az összes kapu megvilágításához. A bekapcsolt lámpák sorszámának meghatározásához a következő algoritmust is használhatjuk.

   Ciklus amíg van meg nem világított kapu
     Keresd meg az első ilyen kaput!
     Határozd meg, melyik az utolsó lámpa, ami megvilágítja!
   Ciklus vége

A bekapcsolt lámpák sorszámát egymástól szóközzel elválasztva jelenítsük meg a képernyőn.

7. A lakók ráébredtek, hogy ez még mindig túl sokba kerül, ezért arra jutottak, hogy egy lámpa csak addig világítson, amíg valaki ebben az utcában tartózkodik, és a fénykörében van. Határozzuk meg, hogy mennyi az egyes lámpák világítási idejének összege, ha valaki 100 méter/perc sebességgel sétál végig az utcán közvetlenül a kerítés mentén. A világítási időt percben jelenítsük meg a képernyőn.

Beküldendő egy tömörített i253.zip állományban a program forráskódja (i253.pas, i253.cpp, ...), valamint a program rövid dokumentációja (i253.txt, i253.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

A beküldési határidő 2011. január 10-én LEJÁRT.

A feladatot érettségi feladatnak szántuk, bár egyes elemeiben - úgy látszik - nehéznek bizonyult.

Néhányan plusz munkát is csináltak maguknak, ellenőrizték a bemeneti fájl meglétét, a v és l kapcsolatát.

A beküldők közül többen nem tudták megfelelően kezelni a adatsorok számát közvetlenül meg nem adó bemeneti fájlt. A szövegfájl utolsó értékes adatot tartalmazó sorának végén is sorvégjel kell álljon. Ennek nem megfelelő kezelése később - jellemzően a a 3. feladat megoldása során - hibát eredményezett.

A 2. feladatot mindenki helyesen oldotta meg.

A 3. feladatban figyelni kellett a bevezető szövegre, amely megadta, hogy a telkek csak az utcafronti kiterjedésükben térnek el.

A 4. feladat szövege sajnos tartalmazott egy zavaró részletet, amelyet értelemszerűen lehetett korrigálni: a fénykör sugarának el kell érnie a lámpatávolság felét - különben egyes területek sötétben maradnának. A v és l értékek viszonyát vizsgáló részt kikommenteltem a fordítás előtt, hogy ki tudjam próbálni más értékekre is.

Az 5. feladatot nehezebbnek gondoltuk, de majdnem mindenki sikerrel birkózott meg vele. Aki hibázott, annak is inkább technikai problémája volt, nem a feladat lényegével adódott gondja.

A 6. feladat megoldását a megadott példa nem segítette kellően. Akik kihasználták a már említett plusz feltételt, nem kellett a példaként adott algoritmust kövessék a megoldás során.

Aki a feltételt nem használta ki, annak számára a megadott algoritmusrészlet lényegének követése (nem feltétlen szolgai megvalósítása) azonban fontos volt. Az első bekapcsolt lámpának az első kaput megvilágítók közül a legnagyobb sorszámúnak kell lennie. A mintamegoldás az egymásba lógó fénykörökre - tehát egy kicsit nehezebb feladatra vonatkozik.

A 7. feladatnál majd minden megoldónak nyilvánvaló volt, hogy a a legelső lámpa nem fog annyi ideig égni, mint a második. Az utolsó lámpa kapcsán már kevesebben gondoltak erre. (Ha az említett feltételt nem használjuk ki, akkor több végéhez közeli lámpa fényköre is kívül eshet az utca végén. A mintaként adott megoldás ezt az eshetőséget is figyelembe veszi.)

A beküldött munkák értékelése az eredeti szöveg figyelembe vételével készült. (A korábbi szöveg attól eltérő kiegészítései a feladat későbbi felhasználása miatt érdekesek.)

Rövidített értékelőlap: i253ertekel.pdf

Tesztfájl: utca.txt

Egy lehetséges megoldás - egymásba nyúló fényköröket tartalmazó, tehát a valóságot jobban megközelítő és ezáltal valamivel nehezebb feladatra: i253.cxx

Statisztika:

10 dolgozat érkezett.
10 pontot kapott:	Hoffmann Áron, Kompis Ádám, Leitereg András, Paróczi Gergő, Szabó 928 Attila.
9 pontot kapott:	Barta 111 János, Gema Barnabás, Kalló Kristóf, Seres Márk Dániel.
7 pontot kapott:	1 versenyző.

A KöMaL 2010. decemberi informatika feladatai