Az I. 292. feladat (2012. április)

I. 292. Egy hatalmas tesztpályán egy robot mozgását kívánjuk vizsgálni a síkban. A robot mozgása a lehető legegyszerűbb, mert egy lépésben a koordináta-rendszer két tengelyének irányába tud elmozdulni. A robot a (0,0) pontból indul, és egy utasítássort hajt végre. Az utasítássor E, H, J és B betűkből áll. Ha a robot az (x,y) pontban van, akkor az E parancs az (x,y+1), a H parancs az (x,y-1), a J parancs az (x+1,y), illetve a B parancs az (x-1,y) pontba viszi át.

A tesztpályán ellenőrzési pontok vannak. A robot az ellenőrzési pontoktól való távolságok összegét minden lépése után feljegyzi. Távolságon a Manhattan-távolságot értjük a feladatban, amely az (x₁,y₁) és (x₂,y₂) pontok esetén |x₁-x₂|+|y₁-y₂|.

A program első parancssori argumentuma legyen egy adatállomány neve. A fájl első sorában N, az ellenőrzési pontok száma () és M, a robot utasításainak száma () van. Az ezt követő N sorban az ellenőrzési pontok x és y koordinátái () vannak szóközzel elválasztva. Az ellenőrző pontok között lehetnek olyanok, amelyeknek mindkét koordinátája megegyezik. A következő sorban M darab karakter (E, H, J, B) van, amely a robot utasítássorát jelenti.

A parancssor második argumentumaként megadott kimeneti állomány M sorban egy-egy egész számot, a robot által az addigi utasítások végrehajtása után feljegyzett távolság-összeget adja.

Például:

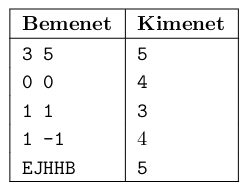
A feladat megoldási ideje 1 másodperc lehet. A tesztpálya mérete és a nagyszámú ellenőrzési pont miatt a hatékony futás érdekében megfelelő előkészítés után érdemes a távolságok összegét számolni.

Beküldendő a program forráskódja (i292.pas, i292.cpp, ...), valamint a program rövid dokumentációja (i292.txt, i292.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

Adrian Satja Kurdija (COCI feladata) nyomán

(10 pont)

A beküldési határidő 2012. május 10-én LEJÁRT.

Megoldásokról:

A beküldött programok egy része minden robotlépés után az összes ellenőrzési pont távolságának összegét újraszámolta. Ezzel a módszerrel a futási idő legfeljebb 1-2000 ellenőrzési pontig és 1-2000 robotlépésig lesz 1 másodperc alatt. Ha az értékek ennél nagyobbak, akkor előfeldolgozást érdemes végezni. Ennek egy lehetséges módszerét Antal János Benjamin (Nyíregyháza, Széchenyi István Közgazdasági Szakközépiskola)12. osztályos tanuló adta meg:

Az adatok beolvasása után feltöltöm a függőleges és vízszintes tömböket. A függőleges tömb i. eleme először azt tartalmazza, hogy hány olyan pont van, amelynek y koordinátája pontosan i. A következő lépésben a függőleges tömb i-dik eleméhez hozzáadok az (i-1). elemet. Így a függőleges tömb azt fogja tárolni, hogy az y=i egyenesen és az alatt hány darab pont van. A vízszintes tömb hasonló lépéseken megy keresztül, csak az x koordinátával, és végül azt fogja tárolni a tömb i. eleme, hogy az x=i egyenesen és attól balra hány pont található. Ez azért fontos, mert a rács bármely részén áll a robot, egy tömbindexeléssel meg lehet mondani, hány pont van tőle balra/jobbra vagy felfelé/lefelé. Ezután megszámolom az összes ellenőrzőpont és a robot távolságát. Minden lépés után csak a következőket csinálom, akár E/H/J/B lépés volt, mindig megnézem a függőleges vagy vízszintes tömb segítségével, hogy a robot lépésének irányában hány pont van a robottól abban az irányban. Ezt a darabszámot kivonom az össztávolságból, mert mindegyik ponthoz 1 egységgel közelebb került. Utána ezt a darabszámot kivonom az N-ből, így megkapom hány ponttól távolodott pontosan 1 egységet. Ezt hozzáadom az össztávolsághoz, és meg is van a lépés utáni távolságok összege anélkül, hogy végig kellett volna számolni az összes pont távolságát.

Mintamegoldása: i292.pas

Tesztállományok: tesztallomanyok.zip

Statisztika:

12 dolgozat érkezett.
10 pontot kapott:	Antal János Benjamin, Jákli Aida Karolina, Kucsma Levente István, Varga 256 Erik.
8 pontot kapott:	1 versenyző.
7 pontot kapott:	3 versenyző.
6 pontot kapott:	2 versenyző.
5 pontot kapott:	2 versenyző.

A KöMaL 2012. áprilisi informatika feladatai