Az I. 337. feladat (2014. január)

I. 337. A jenga népszerű szórakoztató társasjáték, amelyet - kevésbé élvezetes formában - akár online is játszhatunk. A játékszabály elérhetősége http://tarsasoznijo.blog.hu/2009/04/14/jenga, az online játék elérhetősége http://hu.freeonlinegames.com/game/jenga.

Míg a valóságban nagy szerep jut az ügyességnek, a számítógépes változat inkább logikai játéknak tekinthető.

A klasszikus jenga játékkal szemben mi kezdésként n emeletből álló tornyot építünk. Az egyes emeletek felülnézetben felváltva mutatják az alábbi (A/B) szerkezetet:

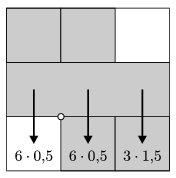
A ledőlés vizsgálatához gondolatban minden jenga elemet bontsunk fel három négyzet alapú hasábra, ezek súlya legyen egységnyi. (Ilyen formában az emeletek közötti szerkezeti különbség eltűnne.) A torony egy hiányos emelet felett dőlhet le. A ledőléshez szükséges állapotot a feladatban úgy definiáljuk, hogy a hiányzó és meglévő elemek találkozásánál lévő ,,alátámasztási'' él hiányos oldalán nagyobb forgatónyomaték lép föl, mint a másikon. A ledőlés vizsgálatát szemlélteti a mellékelt oldalnézeti ábra. Az alsó szint hiányos, az alátámasztási élt ebben a képben a kis kör jelöli. Úgy tekintjük, hogy az egyes elemek tömege a tömegközéppontjukban van. Itt a hiányos oldalon 3 egység a forgatónyomaték (a nehézségi erő 6, az erőkar 0,5 egység), a másik oldalon 7,5 egység a forgatás mértéke (a középső oszlop felett a nehézségi erő 6, az erőkar 0,5 egység, a jobb oldali oszlop felett a nehézségi erő 3, az erőkar 1,5 egység), tehát itt nem dől le a torony. (A számításnál feltettük, hogy a középső szintről egy jenga elem sem hiányzik.)

Írjunk programot, amely a hasábok mozgatás-sorozatát vizsgálva megállapítja, hogy melyik lépés eredményeként dől le a torony. A bemenet első sorában az emeletek száma található. Alatta soronként három adat szerepel egy-egy lépés leírásaként. Az első szám megadja, hogy melyik emeletről veszik el az elemet, a második az adott elem helyét írja le (1/2/3), a harmadik pedig az elhelyezés pozícióját (1/2/3) adja meg. A kimenet megadja a lépés sorszámát és a ledőlés okát: ,,az eltávolítás miatt'', ,,az elhelyezés miatt''.

A program első parancssori argumentuma a bemeneti fájl, a második pedig a kimeneti fájl neve legyen.

Beküldendő egy tömörített i337.zip állományban a program forráskódja (i337.pas, i337.cpp, ...), valamint a program rövid dokumentációja (i337.txt, i337.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2014. február 10-én LEJÁRT.

A feladat kevés versenyzőt vonzott és csak két teljesen helyes megoldás született.

A feladat megoldását megkönnyítette - volna - a játékszabály is, amely szerint csak teljes emelet alól lehet kivenni elemet és az, hogy csak teljes emeletek építhetők. Mivel az elemek itt abszolút pontossággal, súrlódásmentesen mozgathatók - szemben a valósággal, a probléma arra egyszerűsödhet, hogy azon az emeleten, ahonnan az elemet kivesszük, hány elem maradt és hol.

A két legjobban sikerült megoldás Fényes Balázsé (i337fenyes.cs) és Kovács Balázs Marcellé ( i337kovacs.cpp).

Az értékelés során a dokumentáció 2 pontot ért. Az előírásoknak megfelelő program 1 pontot jelentett. A tesztesetekre (i337teszt.zip) helyes megoldásonként 0,5-0,5 pont volt szerezhető.

Statisztika:

5 dolgozat érkezett.
10 pontot kapott:	Fényes Balázs, Kovács Balázs Marcell.
7 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2014. januári informatika feladatai