Az I. 460. feladat (2018. szeptember)

I. 460. Egy téglalap alakú üveglapra gondolatban egy $\displaystyle N\times M$-es ($\displaystyle 10\le N, M\le 10\,000$) négyzethálót helyezünk. Az üveglapot rá merőlegesen $\displaystyle P$ ($\displaystyle 0\le P\le N\times M$) pontban egy-egy nem polarizált fénysugárral megvilágítjuk úgy, hogy minden fénysugár pontosan egy négyzetre essen. Az üveglapra $\displaystyle K$ ($\displaystyle 0\le K\le 1\,000$) darab különböző szélességű és hosszúságú, téglalap alakú polárszűrőt helyezünk el úgy, hogy oldalaik a négyzetháló rácsvonalaira esnek. A polárszűrők érintkezhetnek és átfedhetik egymást, de a lapról nem lóghatnak le. Kétféle polárszűrő van: az egyik a beérkező fényt az üveglap felső oldalával párhuzamosan, a másik arra merőlegesen polarizálja. Az a fénysugár, amely két, egymásra merőlegesen polarizáló polárszűrőre esik, nem jut át az üveglapon.

Készítsünk programot i460 néven, amely a következő problémákat oldja meg.

A program olvassa be a standard input első sorából $\displaystyle N$-et, $\displaystyle M$-et, $\displaystyle P$-t és $\displaystyle K$-t. A következő $\displaystyle P$ sorból a megvilágított négyzetek bal alsó sarkának koordinátáit, utána $\displaystyle K$ sorból a polárszűrők bal alsó, illetve jobb felső sarkának koordinátáit és a polarizációt ($\displaystyle p$ vagy $\displaystyle m$). A koordináták egész számok, az üveglap bal alsó sarkának koordinátái $\displaystyle 1,1$. A program írja a standard output egymás utáni három sorába a következő feladatok megoldását:

– soroljuk fel a beolvasás sorrendjében azoknak a fényforrásoknak a sorszámát, amelyek fénye nem jut át az üveglapon a polárszűrők miatt;

– adjuk meg, hány olyan négyzet van, amelyet nem világítunk meg, de a polárszűrők miatt nem átlátszó;

– adjuk meg, melyek azok a polárszűrők, amelyeket eltávolítva a fénysugarak átlépése nem változik (több lehetséges megoldás esetén elég egyet megadni).

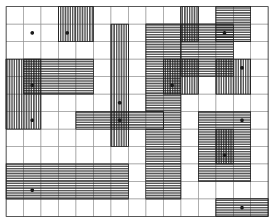
Példa:

Beküldendő egy tömörített i460.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

A beküldési határidő 2018. október 10-én LEJÁRT.

Statisztika:

14 dolgozat érkezett.
10 pontot kapott:	Bálint Ádám, Békési Péter, Horcsin Bálint, Kovács 202 Bertold, Papp Marcell Miklós, Szalay Bálint, Tersztenyák Balázs, Ürmössy Dorottya, Varga 225 Balázs, Vígh Márton, Zámborszky Balázs.
8 pontot kapott:	1 versenyző.
7 pontot kapott:	1 versenyző.
5 pontot kapott:	1 versenyző.

A KöMaL 2018. szeptemberi informatika feladatai