Az I. 552. feladat (2021. december)

I. 552. (É). Az emberiség történelme során többféle számírás és számolási módszer alakult ki. A helyiértékes számrendszer használatának elterjedése előtt a számokat különféle jelekkel, jelcsoportokkal írták le. Az ókori görögöknél az i.\(\displaystyle \,\)e. V. században kialakult alfabetikus számírásban például az ABC betűi jelentették a számokat. A megfeleltetés \(\displaystyle \mathrm{alfa(A)}=1\), \(\displaystyle \text{béta(B)}=2\), \(\displaystyle \ldots\ \)egészen kilencig, majd \(\displaystyle \text{ióta(I)}=10\), \(\displaystyle \mathrm{kappa(K)}=20\) stb. A betűkkel nem jelölt számokat a betűkből álló ,,szavak'' segítségével adták meg: a szó értéke a benne szereplő betűk számértékének összegével volt egyenlő.

Alkalmazzuk az alfabetikus számítást az angol ABC betűire, vagyis \(\displaystyle \mathrm{A}=1\), \(\displaystyle \mathrm{B}=2\), \(\displaystyle \ldots\ \)és végül \(\displaystyle \mathrm{Y}=700\) és \(\displaystyle \mathrm{Z}=800\). A következő feladatokban ezekkel a ,,számokkal'' kell számolni és műveleteket végezni. A számokat minden esetben az angol ABC nagybetűivel jelöljük. A feladatok megoldása során törekedjünk a mintának megfelelő input/output megvalósítására. A bemeneteket nem kell ellenőrizni, azok a leírásnak megfelelő, helyes értékek. A kommunikáció során az ékezetmentes kiírás is elfogadott.

1. Írjuk ki az angol ABC nagybetűit.

2. Írjuk ki a fenti nagybetűkkel jelölt számokat.

3. Kérjünk be a felhasználótól egy számot jelentő betűt, és adjuk meg a számértékét.

4. Kérjünk be a felhasználótól egy számot jelentő szót (legföljebb 10 betű), és adjuk meg a számértékét.

A számok felírása nem egyértelmű, például a 31 felírható LA, AJK vagy akár JDGJ alakban is.

5. Kérjünk be a felhasználótól két számot jelentő szót (legföljebb 10 betű), és adjuk meg, hogy egyenlő értékű-e a két szó.

6. Kérjünk be a felhasználótól egy tízes számrendszerben felírt számot, és adjuk meg a neki megfelelő legrövidebb szavak egyikét.

7. Kérjünk be a felhasználótól egy tízes számrendszerben felírt számot, és adjuk meg a neki megfelelő hárombetűs szavak mindegyikét.

Minta:

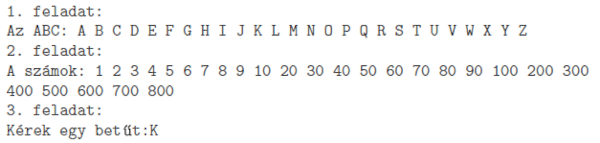
Beküldendő egy i552.zip tömörített állományban a megoldás forráskódja, valamint egy rövid dokumentáció, amely megadja, hogy a program melyik fejlesztői környezetben futtatható.

(10 pont)

A beküldési határidő 2022. január 17-én LEJÁRT.

Mintamegoldásként Gyönki Dominik 9. évfolyamos egri versenyző C++ nyelven készült megoldását (i552.cpp), Nagy Korina kecskeméti, 9. osztályos tanuló Python nyelvű programját (i552.py) adjuk közre.

Statisztika:

8 dolgozat érkezett.
10 pontot kapott:	Gyönki Dominik, Kohut Márk Balázs, Nagy 292 Korina, Simon Tamás, Vadász Levente Márton, Zádor-Nagy Zsombor.
0 pontot kapott:	2 versenyző.

A KöMaL 2021. decemberi informatika feladatai