 |
A K/C. 767. feladat (2023. április) |
K/C. 767. Adott a síkban az ABCD négyzet. A k körvonal áthalad az A, B pontokon és érinti a CD oldalt. Legyen M a k körvonal és a BC oldal B-vel nem azonos metszéspontja. Határozzuk meg a CMBM arány pontos értékét.
Javasolta: Keszegh István (1950–2019)
(5 pont)
A beküldési határidő 2023. május 10-én LEJÁRT.
1. megoldás. Jelöljük a feladatban szereplő kört k-val és legyen a k kör középpontja O. Mivel k az E pontban érinti CD-t, ezért OE merőleges CD-re, de akkor OE egyenese merőleges a CD-vel párhuzamos AB-re is. Az OE tehát a k kör egy átmérőjének egyenese, és ilyen módon az F pontban merőlegesen felezi a kör AB húrját. Ez azt is jelenti, hogy OE merőlegesen felezi a CD szakaszt, vagyis E a CD felezőpontja. Tekintsük az 1. ábrát, amelyen a négyzet oldalát a-val, a CM szakasz hosszát x-szel jelöltük.
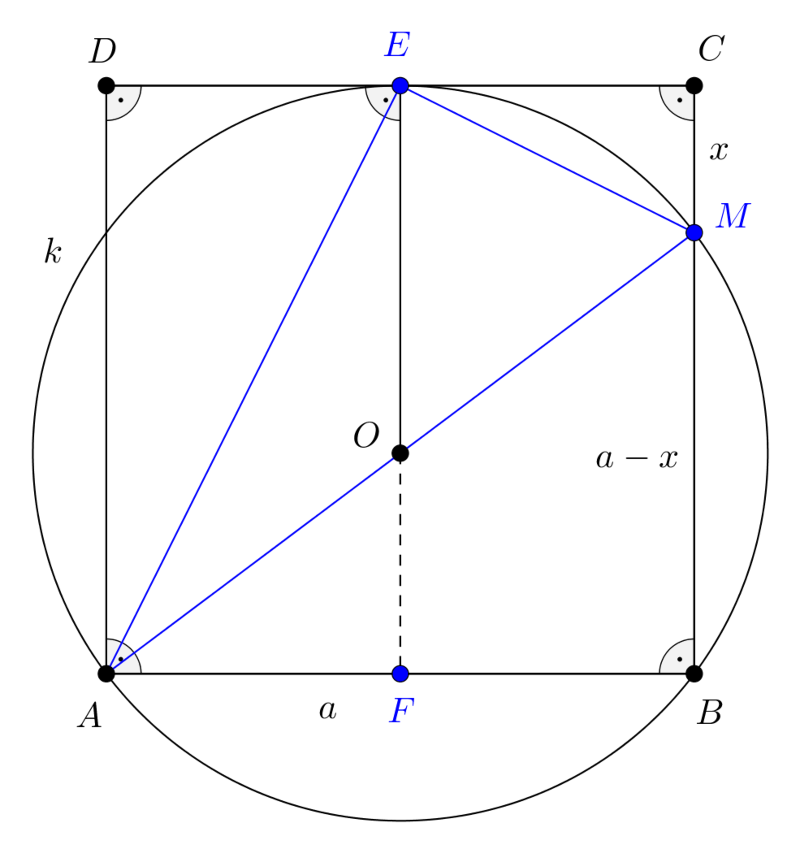
1. ábra
Az AM szakasz áthalad az O ponton, hiszen ABM∢=90∘, így a Thalész-tétel megfordítása miatt AM a kör átmérője. Ebből az is következik, hogy AEM∢=90∘. Az AME derékszögű háromszögre felírjuk a Pitagorasz-tételt:
| (1) | AE2+ME2=AM2. |
Az AED derékszögű háromszögben AD=a és ED=a2, ezért a Pitagorasz-tétel alapján
| (2) | AE2=a2+a24. |
Az EMC derékszögű háromszögből EC=a2 és CM=x felhasználásával a Pitagorasz-tételből
| (3) | ME2=x2+a24 |
következik.
Végül az AMB derékszögű háromszögből AB=a és BM=a−x; a Pitagorasz-tétel miatt
| (4) | AM2=a2+(a−x)2. |
Behelyettesítjük a (2)-(3)-(4) eredményeket az (1) egyenletbe:
a2+a24+x2+a24=a2+(a−x)2,
ahonnan a műveletek elvégzésével és rendezéssel
x=a4
következik. Ez azt jelenti, hogy
CMBM=a43a4=13,
tehát az M pont a BC szakasz C-hez legközelebbi negyedelőpontja.
2. megoldás. Az 1. megoldásban látott módon igazolhatjuk, hogy E felezőpontja a CD szakasznak és az AM szakasz átmérő az O középpontú k körben, emiatt AEM∢=90∘.
A következő ábrán a CME∢=α és az MEC∢=β jelöléseket alkalmaztuk, amelyekre nyilvánvalóan teljesül, hogy
α+β=90∘.
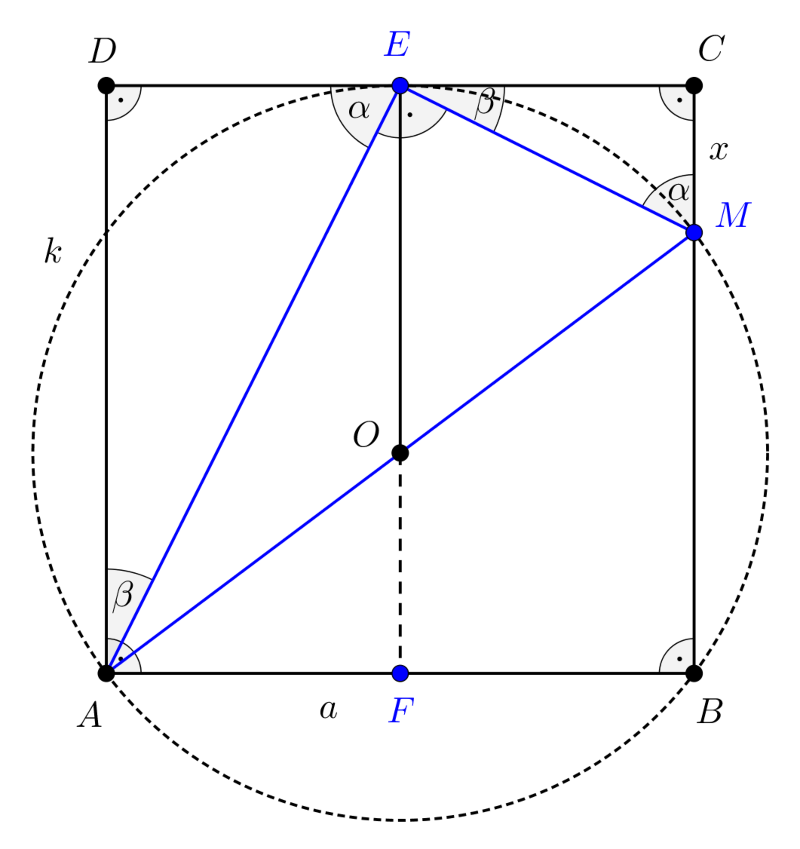
2. ábra
Az α+β=90∘ összefüggés miatt AED∢=α és így DAE∢=β.
Az EMC és AED derékszögű háromszögek megfelelő szögei egyenlők, ez a két háromszög tehát hasonló, ezért a két háromszög megfelelő oldalainak aránya megegyezik. Eszerint: CMCE=EDAD, azaz xa2=a2a.
Ebből a műveletek elvégzése és egyszerűsítés után adódik, hogy
x=a4,
vagyis az M pont a BC szakasz C-hez legközelebbi negyedelőpontja, tehát
CMBM=13.
Statisztika:
92 dolgozat érkezett. 5 pontot kapott: 54 versenyző. 4 pontot kapott: 4 versenyző. 3 pontot kapott: 14 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 9 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2023. áprilisi matematika feladatai
|
|

