A K/C. 797. feladat (2024. január)

K/C. 797. Egy 10 cm befogójú, egyenlő szárú derékszögű háromszög befogói és átfogói mint átmérők fölé rajzolunk egy-egy kört. Az egyik körlapot kiszínezzük pirosra, a másikat kékre, a harmadikat zöldre. Mennyi a területe a legalább két színnel színezett síkrésznek?

(5 pont)

A beküldési határidő 2024. február 12-én LEJÁRT.

Megoldás. Készítsünk ábrát, amelyről leolvashatjuk, hogy a legalább két színnel színezett síkrész éppen a nagyobbik kör feléből és két egybevágó körszeletből áll.

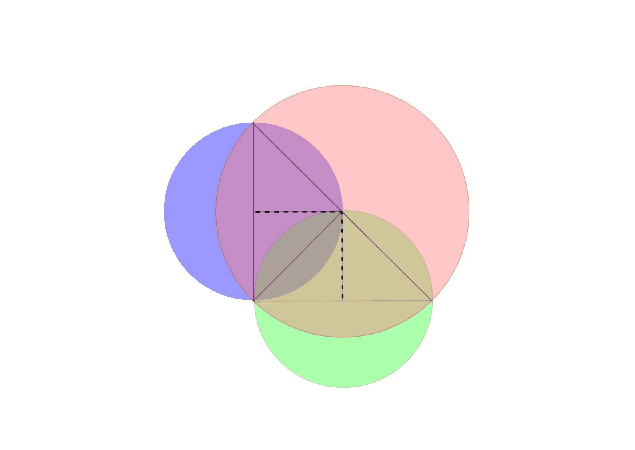
Pitagorasz tételét felhasználva kiszámoljuk a nagyobbik kör sugarát: \(\displaystyle R=5 \sqrt{2}\) cm. Így a nagy félkör területe:

\(\displaystyle T_{\text{félkör}}=\frac{R^2\pi}{2}=25 \pi ~\text{cm}^2.\)

A két színnel jelölt körszeletek mindegyike a kisebb körökben éppen egy \(\displaystyle 90^{\circ}\)-os középponti szöghöz tartozik, így területét meghatározhatjuk úgy, hogy a kisebb kör területének negyedéből kivonjuk a kis, \(\displaystyle 5\) cm befogójú derékszögű háromszög (az ábrán az egyik befogója szaggatott) területét:

\(\displaystyle T_{\text{körszelet}}=\frac{5^2\pi}{4}-\frac{5^2}{2}=6,\!25 \pi-12,\!5 ~\text{cm}^2.\)

A keresett terület nagysága tehát

\(\displaystyle T=T_{\text{félkör}}+2 \cdot T_{\text{körszelet}}=25 \pi + 12,\!5 \pi-25=37,\!5 \pi -25 \approx 92,\!81 ~\text{cm}^2.\)

Statisztika:

196 dolgozat érkezett.
5 pontot kapott:	77 versenyző.
4 pontot kapott:	36 versenyző.
3 pontot kapott:	15 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	4 versenyző.
Nem versenyszerű:	3 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	51 dolgozat.

A KöMaL 2024. januári matematika feladatai