 |
A K. 164. feladat (2008. március) |
K. 164. Egy körvonalon felvettünk nyolc pontot, a szomszédos pontok egymástól egyenlő távolságra vannak. Olyan nem egyenlő szárú háromszöget rajzolunk, amelynek mindhárom csúcsa a nyolc pont egyike. Mekkorák lehetnek a háromszög szögei?
(6 pont)
A beküldési határidő 2008. április 10-én LEJÁRT.
Megoldás: A nyolc pontot felhasználva ötféle különböző háromszög készíthető, ezek közül kettő nem egyenlő szárú (lásd az ábrán).
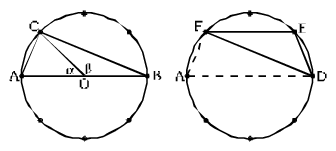
Az ABC háromszögben AB átmérő, ezért C-nél a Thalesz-tétel értelmében derékszög van. Az  -val jelölt szög a teljes szög nyolcadrésze, azaz 45o, így az OAC egyenlő szárú háromszög alapon fekvő szögei 67,5o nagyságúak, tehát a CAB szög nagysága 67,5o. Az ABC háromszög harmadik szöge 22,5o-os.
-val jelölt szög a teljes szög nyolcadrésze, azaz 45o, így az OAC egyenlő szárú háromszög alapon fekvő szögei 67,5o nagyságúak, tehát a CAB szög nagysága 67,5o. Az ABC háromszög harmadik szöge 22,5o-os.
A DEF háromszöget az első ábrán látható háromszöggel egy húrtrapézzá tudjuk kiegészíteni. A húrtrapéz D-nél levő szöge 67,5o nagyságú, ezért az E-nél levő szög nagysága 112,5o. A DEF háromszög D-nél levő szöge a 67,5o (a húrtrapéz alapon fekvő szöge) és a 22,5o (az ADF háromszög D-nél levő szöge) különbsége, azaz 45o. A DEF háromszög harmadik szöge 22,5o.
Statisztika:
129 dolgozat érkezett. 6 pontot kapott: Almási Péter, Árvay Balázs, Balogh 411 Péter, Balogh Beáta, Bartha Kristóf, Benkő Anna, Bicskei Dávid, Blóz Gizella Evelin, Botond Ákos, Csapó Botond, Csernyánszky Nándor, Czebe 007 Brigitta, Czinder Gábor, Dúzs Brigitta, Engert János Dávid, Farkas Zoltán, Haléder Zsuzsanna, Hegedűs Csaba, Jezeri András, Kaplár F. Benedek, Kiss 992 László, Kunos Vid, Medvey Fanni, Mihálykó András, Nagy-György Péter, Nahaj Judit, Palotás Julianna, Pánczél János Károly, Pós Eszter Sarolta, Rudas Csilla, Sass Zoltán, Schwarcz Gergő, Szatmári György, Szinger Árpád, Tamás Ádám, Ván Bálint, Varga 777 Ádám, Várnai Péter, Zempléni Réka. 5 pontot kapott: 44 versenyző. 4 pontot kapott: 9 versenyző. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 10 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 12 versenyző. Nem versenyszerű: 4 dolgozat.
A KöMaL 2008. márciusi matematika feladatai
