 |
A K. 165. feladat (2008. március) |
K. 165. Balázs és Zsófi papírcsíkokból karikákat gyártanak, majd ezeket összefűzve láncot készítenek. Mindketten egy 21×30 cm-es papírlapot használnak fel a lánc elkészítéséhez. Balázs a 21 cm-es oldallal párhuzamosan, Zsófi a 30 cm-es oldallal párhuzamosan 1 cm széles csíkokra vágja fel a papírt. A kapott csíkok végeit egymáshoz érintve karikákat ragasztanak össze átfedés nélkül. A karikák láncszerűen kerülnek egymásba úgy, hogy közben nem deformálódnak. Melyikük lánca lett hosszabb? (A kör kerületének számításakor a  értékét vegyük 3,14-nak; a papírlap vastagságát vegyük nullának.)
értékét vegyük 3,14-nak; a papírlap vastagságát vegyük nullának.)
(6 pont)
A beküldési határidő 2008. április 10-én LEJÁRT.
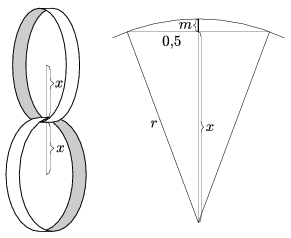
I. megoldás: Balázs 21 cm hosszú papírcsíkokat vág, és ebből van neki 30 db. Mivel a ragasztásnál nincs átfedés, egy karikájának sugara cm. Mint az ábrán látszik, a karikák a találkozásuknál megemelik egy kicsit egymást annyival, amekkora egy 1 cm-es húr által levágott körszelet m magassága. Az ábrán x=r-m jelöli azt a hosszt, amivel számolnunk kell a lánc hosszának megállapításakor. A Pitagorasz-tétel alkalmazásával:
cm. A 30 db karika 30.2.3,30+31.(3,34-3,30)=199,24 cm hosszú láncot alkot.
Zsófi 30 cm hosszú papírcsíkokat vág, és ebből van neki 21 db. Egy karikájának sugara cm, amiből x=4,75 cm, a 21 db karika tehát 21.2.4,75+22.(4,78-4,75)=200,16 cm hosszú láncot alkot. Tehát Zsófi lánca hosszabb, mint Balázsé.
II. megoldás: Balázs karikájának kerülete kevesebb (21 cm), mint Zsófi karikájának kerülete (30 cm). Egy kisebb kerületű körlemezből ugyanolyan hosszú húr (1 cm) nagyobb magasságú körszeletet vág le, mint egy nagyobb kerületűből. Tehát egy 21 cm kerületű karikákból készülő lánc többet veszít a hosszából, mint egy ugyanannyi darab 30 cm kerületű karikából álló lánc. Balázsnak ráadásul több karikája is van (30 darab), mint Zsófinak (21 darab), tehát a lánca még többet veszít a hosszából. Ezek alapján Zsófi lánca hosszabb lesz, mint Balázsé.
Statisztika:
144 dolgozat érkezett. 6 pontot kapott: Csernyánszky Nándor, Hegedűs Csaba, Pánczél János Károly, Pere Tamás, Tene Zsuzsanna, Varga 777 Ádám. 5 pontot kapott: Blóz Gizella Evelin, Kunos Vid, Rudas Csilla, Várnai Péter. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 122 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2008. márciusi matematika feladatai
