A K. 188. feladat (2008. december)

K. 188. Az ABC egyenlő szárú háromszög AB alapját a B csúcson túl meghosszabbítottuk a szár hosszával. Az így kapott pont lett a C₁. Az AB alapra az A csúcsban merőlegest állítottunk, majd a C-t tartalmazó félsík irányába a merőleges egyenesre felmértük a szár hosszát. Az így kapott pont lett a C₂. Azt tapasztaltuk, hogy a C₁, C és C₂ pontok egy egyenesre illeszkednek. Határozzuk meg az ABC háromszög szögeit.

(6 pont)

A beküldési határidő 2009. január 10-én LEJÁRT.

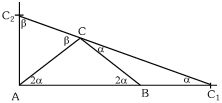
Megoldás. A vázlatrajzon bejelöljük a szögeket. CC₁B szög legyen , CC₂A szög legyen . Mivel CC₁B és CC₂A háromszögek egyenlő szárúak, ezért a C pontnál az ábrán jelölt módon megjelenik és . Mivel C₁, C és C₂ pontok egy egyenesre illeszkednek, ezért a C-nél 180^o-os szög van. C₁AC₂ háromszög derékszögű, így +=90^o, tehát az ABC háromszög C-nél levő szöge is 90^o-os. Az ABC háromszög egyenlő szárú, tehát szögei: 45^o, 45^o, 90^o.

Statisztika:

166 dolgozat érkezett.
6 pontot kapott:	110 versenyző.
5 pontot kapott:	14 versenyző.
4 pontot kapott:	6 versenyző.
3 pontot kapott:	5 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	13 versenyző.
Nem versenyszerű:	7 dolgozat.

A KöMaL 2008. decemberi matematika feladatai