 |
A K. 213. feladat (2009. szeptember) |
K. 213. Egy téglalapot az oldalaival párhuzamos vágásokkal kilenc darabra vágtunk. Az egyes darabokba beleírtuk a területüket cm2-ben kifejezve. Mennyi az x-szel jelölt darab területe?
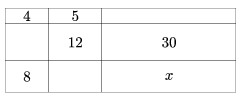
(6 pont)
A beküldési határidő 2009. október 12-én LEJÁRT.
1. megoldás. Felhasználjuk, hogy az egy sorban levő téglalapok területének az aránya az oszlopok szélességének az arányával egyezik meg. Ugyanígy az azonos oszlopban levő téglalapok területének aránya a sorok magasságának arányával egyezik meg. Így az első sor utolsó téglalapjának területe \(\displaystyle \frac{30}{12}\cdot 5 = 12,5\).
Mivel az első oszlop alsó téglalapja kétszer akkora területű, mint a felső, ezért ez áll a harmadik oszlop megfelelő celláinak területére is. Tehát \(\displaystyle x=25\).
2. megoldás. Ha a téglalap vízszintes oldala \(\displaystyle u\), \(\displaystyle v\), \(\displaystyle w\) nagyságú részekre, a függőleges pedig \(\displaystyle p\), \(\displaystyle q\), \(\displaystyle s\) nagyságú részekre van szétvágva, akkor \(\displaystyle v=\frac54 u\), \(\displaystyle w=\frac{30}{12} v=\frac{30}{12} \cdot \frac54 u=\frac{25}{8} u\), továbbá \(\displaystyle q=\frac{12}{5} p\) és \(\displaystyle s=2p\). Így \(\displaystyle x=ws=\frac{25}{8} u\cdot 2p=\frac{25}{4} up=\frac{25}{4} \cdot 4=25\).
Statisztika:
282 dolgozat érkezett. 6 pontot kapott: 127 versenyző. 5 pontot kapott: 58 versenyző. 4 pontot kapott: 21 versenyző. 3 pontot kapott: 52 versenyző. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 5 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2009. szeptemberi matematika feladatai
