A K. 258. feladat (2010. szeptember)

K. 258. Az egyszerűsíthető (pozitív értékű) törtben az x pozitív egész számot jelöl. Hányféle értéket vehet fel az x?

(6 pont)

A beküldési határidő 2010. október 11-én LEJÁRT.

Megoldás. Az \(\displaystyle \frac{1000-x}{1001}\) tört pontosan akkor egyszerűsíthető, ha a számláló \(\displaystyle 1000-x\)-nek és a nevező \(\displaystyle 1001\)-nek van közös 1-nél nagyobb osztója. Mivel \(\displaystyle 1001=7\cdot 11\cdot 13\), ezért az 1-nél nagyobb osztói a \(\displaystyle 7\), \(\displaystyle 11\), \(\displaystyle 13\), \(\displaystyle 77\), \(\displaystyle 91\), \(\displaystyle 143\) és \(\displaystyle 1001\). Mivel \(\displaystyle x\) pozitív, ezért \(\displaystyle 1000-x\) kisebb \(\displaystyle 1001\)-nél, így az nem lehet az osztója.

Az 1000-nél kisebb 7-tel osztható pozitív számok száma (7-től 994-ig) \(\displaystyle 994/7=142\).

Az 1000-nél kisebb 11-gyel osztható pozitív számok száma (11-től 990-ig) \(\displaystyle 990/11=90\).

Az 1000-nél kisebb 13-mal osztható pozitív számok száma (13-tól 988-ig) \(\displaystyle 988/13=76\).

Az 1000-nél kisebb 77-tel osztható pozitív számok száma (77-től 924-ig) \(\displaystyle 924/77=12\).

Az 1000-nél kisebb 91-gyel osztható pozitív számok száma (91-től 910-ig) \(\displaystyle 910/91=10\).

Az 1000-nél kisebb 143-mal osztható pozitív számok száma (143-tól 858-ig) \(\displaystyle 858/143=6\).

Amikor összeszámoltuk a 7-tel vagy a 11-gyel osztható számok számát, akkor mindkét esetben találkoztunk olyanokkal, melyek mindkettővel oszthatóak, azaz 77-tel is. Ugyanezt elmondhatjuk a másik két esetben (7 és 13, ill. 11 és 13) is. Például \(\displaystyle x=76\) esetében a \(\displaystyle 924\)-et a 7-tel osztható és a 11-gyel osztható számok között is megszámoltuk. Az olyan számok száma, melyek csak 7-tel oszthatóak, de 11-gyel nem \(\displaystyle 142-12=130\). Olyan legfeljebb háromjegyű pozitív szám, mely 11-gyel osztható, de 7-tel nem \(\displaystyle 90-12=78\) darab van. Ugyanilyen módon a többi párra is megállapításokat tehetünk.

Mivel \(\displaystyle 7\cdot 11\cdot 13=1001>1000\), egyetlen olyan számunk sem volt, melynek mind a 7, mind a 11 és mind a 13 osztója lett volna egyszerre. Ezért a következő halmazábrát rajzolhatjuk le, mely a különböző halmazok elemszámát tartalmazza:

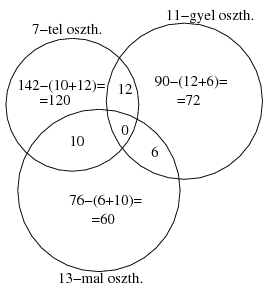
Az 1000-nél kisebb 1001 1-nél nagyobb osztóival osztható számok összes száma \(\displaystyle 120+72+60+12+10+6=280\).

A halmazábra elkészítése nélkül az ún. logikai szitával kiszámolva (ennek volt képiesített ás illusztrált változata a fenti ábra) a megfelelő számok száma \(\displaystyle 142+91+76-12-10-6+0=280\).

Statisztika:

288 dolgozat érkezett.
6 pontot kapott:	146 versenyző.
5 pontot kapott:	13 versenyző.
4 pontot kapott:	8 versenyző.
3 pontot kapott:	18 versenyző.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	64 versenyző.
0 pontot kapott:	23 versenyző.
Nem versenyszerű:	8 dolgozat.

A KöMaL 2010. szeptemberi matematika feladatai