A K. 355. feladat (2012. december)

K. 355. Legyen az ABCD négyzet AB oldalán az A-hoz közelebbi harmadoló pont F, az AD oldalán a D-hez közelebbi harmadoló pont E, a CD oldalán a C-hez közelebbi hatodoló pont pedig G. Milyen arányban osztják egymást az EFBG négyszög átlói?

(6 pont)

A beküldési határidő 2013. január 10-én LEJÁRT.

Megoldás. Illesszünk a négyzetre egy 6x6-os négyzetrácsot!

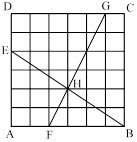
A \(\displaystyle BE\) szakasz \(\displaystyle B\)-től indulva balra hat kis négyzetnyit, felfelé pedig négyet halad, így átmegy a \(\displaystyle B\)-től balra három, felfelé két négyzetnyire levő \(\displaystyle H\) rácsponton. Az \(\displaystyle FG\) szakasz az \(\displaystyle F\)-től indulva jobbra három, felfelé hat kis négyzetnyit halad, így átmegy az \(\displaystyle F\)-től jobbra egy, felfelé kettő négyzetnyire levő \(\displaystyle H\) ponton. Mivel a \(\displaystyle BE\) és \(\displaystyle FG\) szakaszok is átmennek a \(\displaystyle H\) ponton, ezért metszéspontjuk \(\displaystyle H\). A \(\displaystyle H\) pont harmadolja \(\displaystyle FG\)-t, és felezi \(\displaystyle BE\)-t, így a két átló \(\displaystyle 1:1\), illetve \(\displaystyle 1:2\) arányban osztja egymást.

Statisztika:

100 dolgozat érkezett.
6 pontot kapott:	Baglyas Márton, Balog 6 Klaudia, Bauer Márton, Bodonhelyi Anna, Bottlik Judit, Coulibaly Patrik, Csatári Jakab, Cserna Koppány Levente, Dani Máté, Galbács Márton, Garaba Flórián, Ghyczy András, Gruber 717 Enikő, Horváth 016 Gábor, Ipolyszegi Gábor, Juhász 326 Dániel, Kasó Gergő, Keszthelyi Máté, Kis Levente, Kocsis Júlia, Kocsis-Savanya Miklós, Kozma-Bognár Levente, Matusek Márton, Mészáros 01 Viktória, Mihálykó Péter, Németh Flóra Boróka, Pálfi Mária, Papp 535 Ágnes, Pintér Gergő, Ratkovics Gábor, Sevella Dénes, Stefics Attila, Stumphauser Nóra, Szabó Bettina, Szabó Júlia, Szalai Tibor Viktor, Szántó Benedek, Szentgyörgyi Flóra, Szili Dániel, Szűcs Áron Ábrahám, Tóth Bálint, Varga 123 Péter.
5 pontot kapott:	Blum Balázs, Domokos Vanessza, Hegedűs Henrietta, Ivankoviæ Mladen, Mári László Levente, Marticsek Réka.
4 pontot kapott:	11 versenyző.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	10 versenyző.
1 pontot kapott:	18 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2012. decemberi matematika feladatai