 |
A K. 358. feladat (2012. december) |
K. 358. Egy raktárban azonos tömegű és méretű, kocka alakú dobozok vannak összerendezve téglatest formára. A munkás, aki azt a feladatot kapta, hogy rakja fel ezeket egy teherautóra, egyszerre egy doboz vastagságának megfelelő függőleges vagy vízszintes irányú réteget pakol fel az autóra. (A dobozokhoz bármelyik irányból hozzá tud férni.) A dobozok tömege kilogrammban mérve egész szám. Az elsőként bepakolt dobozok összes tömege 60 kg, a másodszor bepakoltaké 84 kg, a harmadszor bepakoltaké 112 kg. Hány kg lehet az összes doboz tömege együttesen?
(6 pont)
A beküldési határidő 2013. január 10-én LEJÁRT.
Megoldás. Mivel egy doboz tömege kg-ban mérve egész szám, ezért osztója 60-nak, 84-nek és 112-nek is. A számok prímtényezős felbontását megvizsgálva a szóba jöhető értékek: 1, 2 és 4 kg. A pakolás során egyre több dobozt rakott be az egyes fázisokban, ezért ez három különböző irányú réteget jelentett (azaz semelyik kettő közülük nem párhuzamos helyzetű egymással). Legyenek a téglatest élei a, b és c doboz hosszúságúak. Az általánosságot nem szorítja meg, ha a bepakolt rétegekben levő dobozok darabszámát \(\displaystyle ab\), \(\displaystyle a(c–1)\), \(\displaystyle (c–1)(b–1)\) jelöli. (Most \(\displaystyle b, c \geq 2\), viszont \(\displaystyle a = 1\) lehetséges; ha a téglatest két vagy három éle 1 doboznyi lenne, akkor az első vagy a második berakásnál elfogynának a dobozok, és nem tudnánk folytatni.)
1.eset: Egy doboz tömege 1 kg. Ekkor a tömegekre vonatkozó összefüggésekből \(\displaystyle ab = 60\), \(\displaystyle \frac{a}{b-1}=\frac{84}{112}=\frac34\). Ha a 60 osztópárjait megvizsgáljuk (az \(\displaystyle a < b\) eseteket, mert ha \(\displaystyle b\)-ből 1-et levonunk, akkor még mindig nagyobb lesz \(\displaystyle a\)-nál), akkor nem találunk megfelelő párokat:

2.eset: Egy doboz tömege 2 kg. Ekkor a fentiekhez hasonlóan \(\displaystyle ab = 30\), \(\displaystyle \frac{a}{b-1}=\frac34\). Ha a 30 osztópárjait megvizsgáljuk (az \(\displaystyle a < b\) eseteket, mert ha \(\displaystyle b\)-ből 1-et levonunk, akkor még mindig nagyobb lesz \(\displaystyle a\)-nál), akkor nem találunk megfelelő párokat:

3.eset: Egy doboz tömege 4 kg. Ekkor a fentiekhez hasonlóan \(\displaystyle ab = 15\), \(\displaystyle \frac{a}{b-1}=\frac34\). Ha a 15 osztópárjait megvizsgáljuk (az \(\displaystyle a < b\) eseteket, mert ha \(\displaystyle b\)-ből 1-et levonunk, akkor még mindig nagyobb lesz \(\displaystyle a\)-nál), akkor egy megfelelő értékpárt találunk:
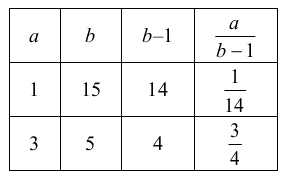
Tehát egyetlen megoldásként kapjuk, hogy \(\displaystyle a = 3\), \(\displaystyle b = 5\). Ellenőrizhető, hogy a hozzájuk kiszámítható \(\displaystyle c = 8\) mindkét további feltételnek megfelel. Így a dobozok összes száma \(\displaystyle 3\cdot5\cdot8 = 120\) volt, összes tömegük pedig 480 kg.
Statisztika:
109 dolgozat érkezett. 6 pontot kapott: Bagosi Lívia, Bálint Roland Péter, Berekai Eszter, Bodonhelyi Anna, Bottlik Judit, Coulibaly Patrik, Csatári Jakab, Cserna Koppány Levente, Farkas Olivér, Garaba Flórián, Hegedűs Henrietta, Horváth 016 Gábor, Horváth Emma, Juhász 326 Dániel, Kaprinai Ádám, Kasza Bence, Kis Levente, Kocsis Júlia, László Márton, Márton Tamás, Mészáros 01 Viktória, Mihálykó Péter, Németh Flóra Boróka, Pálfi Mária, Papp 535 Ágnes, Pintér Gergő, Pipis Bence, Stark Patrícia, Szabó 11 Dániel, Szathmári Balázs, Szűcs Kilián Ádám, Szücs Patrícia, Tauber Boglárka, Varga 123 Péter, Vecseri Bence, Záhonyi Petra. 5 pontot kapott: 20 versenyző. 4 pontot kapott: 10 versenyző. 3 pontot kapott: 12 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 9 versenyző. 0 pontot kapott: 18 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2012. decemberi matematika feladatai
