A K. 389. feladat (2013. október)

K. 389. Adott a koordinátarendszerben egy F betűt formázó alakzat, melynek csúcsait az alábbi koordináták határozzák meg: (0;2), (3;2), (3;1), (1;1), (1;0), (2;0), (2;-1), (1;-1), (1;-4), (0;-4). Adjuk meg annak az elsőfokú függvénynek a hozzárendelési szabályát, amelynek a grafikonja felezi az F betű területét.

(6 pont)

A beküldési határidő 2013. november 11-én LEJÁRT.

Megoldás. A kitűzésből kimaradt, hogy az egyenes origón átmenő, így nyilván bármilyen meredekséggel megadható megfelelő egyenes, vagyis végtelen sok megoldás van. Aki egyet megadott megfelelő indoklással, az megkapja a 6 pontot.

Például Asztalos Márton (Budapest, Berzsenyi D. Gimn.) megoldása is jó:

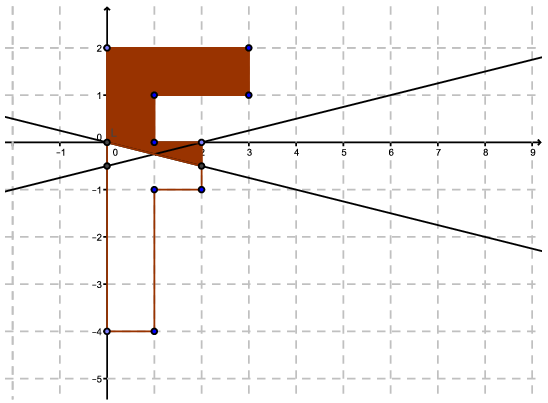
A megrajzolt \(\displaystyle F\) betű az ábrán látszik. A területe 9. Tehát olyan elsőfokú fügvényt kéne találni, ami az \(\displaystyle F\) betű területét két 4,5 területű részre osztja.

A két talált függvény nagyon hasonló: \(\displaystyle y=0,25x-0,5\) és \(\displaystyle y=-0,25x\) – ez utóbbi origón átmenő egyenes. Mindkét esetben az előző felezéskor keletkezett ,,felső" területből elveszünk és hozzáadunk egy-egy nyolcad egységnégyzetet, így a terület marad 4,5.

Statisztika:

198 dolgozat érkezett.
6 pontot kapott:	91 versenyző.
5 pontot kapott:	27 versenyző.
4 pontot kapott:	4 versenyző.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	30 versenyző.
1 pontot kapott:	15 versenyző.
0 pontot kapott:	15 versenyző.
Nem versenyszerű:	9 dolgozat.

A KöMaL 2013. októberi matematika feladatai