 |
A K. 477. feladat (2015. november) |
K. 477. Jancsi éppen azt tanulja, hogyan kell evőpálcikákkal enni. Gyakorlásképpen a két összefogott evőpálcikával egy 4 cm átmérőjű golyót kell felvennie az ábrán látható módon. (A gömböt akkor lehet felemelni, ha középpontja illeszkedik a pálcikák által meghatározott síkra.) A két evőpálcika Jancsi kezében éppen 60 fokos szöget zár be egymással. Mekkora távolságra van az akció során a pálcikák találkozási pontjától a gömb (ehhez a ponthoz) legközelebbi pontja?
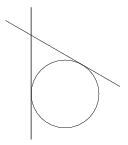
(6 pont)
A beküldési határidő 2015. december 10-én LEJÁRT.
Megoldás. Ábránkon az a síkmetszet látható, amely tartalmazza a két pálcikát. A síkmetszeten a kör sugara megegyezik a golyó főkörének sugarával, ami 2 cm. A keresett \(\displaystyle K\) pont a két egyenes \(\displaystyle P\) metszéspontját a kör \(\displaystyle O\) középpontjával összekötő szakasz és a kör metszéspontja.
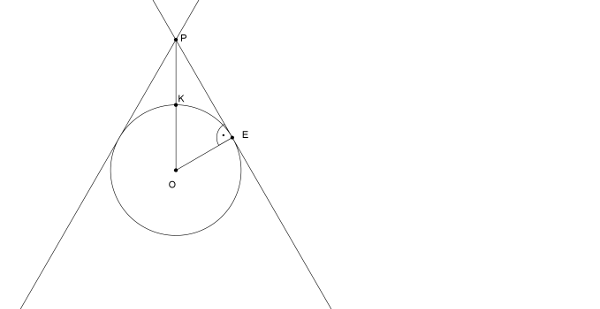
Jelölje \(\displaystyle O\) az egyik pálcikán lévő érintési pontot. Tudjuk, hogy az érintő merőleges az érintési pontban húzott sugárra, így \(\displaystyle OEP\angle=90^{\circ}\). Mivel a \(\displaystyle PO\) egyenes felezi a két pálcika egyenese által bezárt szöget, ezért a \(\displaystyle POE\) háromszögben a \(\displaystyle P\) csúcsnál lévő szög a \(\displaystyle 60^{\circ}\) fok fele, vagyis \(\displaystyle 30^{\circ}\). A háromszög \(\displaystyle E\) csúcsánál pedig derékszög van. Tehát a háromszög egy szabályos háromszög fele, és így \(\displaystyle OP=2OE=2\cdot2=4\) cm. Ebből le kell vonnunk a kör sugarát, hogy megkapjuk a keresett távolságot.
Tehát a gömb legközelebbi pontja \(\displaystyle 4-2=2\) cm-re van a pálcikák metszéspontjától.
Statisztika:
109 dolgozat érkezett. 6 pontot kapott: Aradi Sára Katalin, Barta Ákos, Bertók Zsanett, Cseke Tibor, Csikós-Nagy Máté, Csóka Zoárd, Csontos Lilla Ágnes, Czeba Zsolt, Dékány Barnabás, Dobák Dániel, Farkas Norbert, Földvári Ádám, Gárdonyi Csilla Dóra, Giorgos Nikiforakis, Hegedüs Péter, Hoffmann Balázs, Horváth Balázs Máté, Kertész Ferenc, Kiss 468 Péter, Kluèka Vivien, Kovács 161 Márton Soma, Kovács Levente András, Kozma Bianka, Köpenczei Csenge, Lapu Kolos, Marshall Tamás, Máté 446 Dávid, Mester Gyöngyvér, Miskolczi Abigél, Nagy Csaba Jenő, Nemes Balázs Boldizsár, Németh 728 Ágnes Sára, Pálvölgyi Szilveszter, Piller Ádám, Pinke Jakab Zoltán, Rubovszky Cecília , Sal Dávid, Simon Dóra, Szalai Regina, Szöllősi Brigitta, Veress Luca, Zentai Flóra, Zsótér Laura. 5 pontot kapott: 26 versenyző. 4 pontot kapott: 21 versenyző. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2015. novemberi matematika feladatai
