Problem K. 515. (October 2016)

K. 515. Each side of a regular hexagon is extended to the double of its length in the same direction around the clock. The points obtained are connected to form a new hexagon. By what factor is the area of the new hexagon greater than the area of the original hexagon?

(6 pont)

Deadline expired on November 10, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit és legyen az eredeti szabályos hatszög oldalának hossza \(\displaystyle a\). Vizsgáljuk meg a meghosszabbítás során keletkezett háromszögek egyikét, a \(\displaystyle BA’B’\) háromszöget. A háromszög \(\displaystyle CA’\) súlyvonala két egyenlő területű részre osztja a háromszöget, jelölje ezt a területet \(\displaystyle t\). A \(\displaystyle BA’B’\) háromszög területe ezért \(\displaystyle 2t\), a tükrözéssel keletkező hat háromszög együttes területe tehát \(\displaystyle 6\cdot2t=12t\).

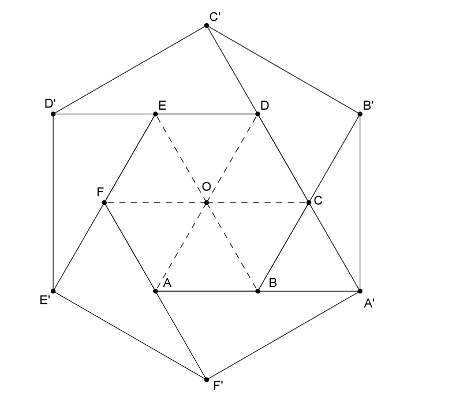
A szabályos hatszög minden szöge \(\displaystyle 120^{\circ}\). Mivel az a \(\displaystyle CBA’\) háromszögben \(\displaystyle CBA’\angle=180^{\circ}-ABC\angle=180^{\circ}-120^{\circ}=60^{\circ}\), és \(\displaystyle BA’=BA=BC=a\), ezért a \(\displaystyle CBA’\) háromszög \(\displaystyle a\) oldalú szabályos háromszög. Az eredeti hatszög \(\displaystyle O\) szimmetria középpontját a csúcsokkal összekötve, a hatszöget hat darab \(\displaystyle a\) oldalú szabályos háromszögre osztjuk, ezek együttes területe \(\displaystyle 6t\).

A területek aránya tehát \(\displaystyle (12t+6t) : 6t = 18 : 6 = 3 : 1\), vagyis az így létrejött hatszög területe háromszorosa az eredeti hatszögének.

Megjegyzés. A feladat az 1988. évi Arany Dániel Matematikaverseny 1. fordulójának 2. feladata volt.

Statistics:

126 students sent a solution.
6 points:	Adravecz Balázs, Antics Hilda, Balogh Bence, Bárdos Deák Botond, Benczik Ákos , Biró András, Bohus Ádám, Bottlik Domonkos, Csóti Kristóf, Demcsák Ágnes, Espán Márton, Fenyvesi Tamás, Gém Viktória, Gion Áron, Gyuricza Gergő, Halász 237 Lajos, Horváth 237 Lili, Juhász 315 Dorka, Juszt Anna, Kis 194 Károly, Kiss 014 Dávid, Kovács 124 Kinga, Kovács 615 Dorina, Kovács Fruzsina Dóra, Kozák 023 Áron, Kozmér Barbara, Lovász Marcell, Lukács Emma, Makszin Mátyás, Markó Gábor, Mátravölgyi Bence, Mendei Barna, Német Franciska, Oláh Zsófia, Op Den Kelder Júlia, Paróczai Anett, Réz 426 Dávid, Rozgonyi Gergely, Rusvai Miklós, Sepsi Csombor Márton, Simai Anna Éva, Szilágyi Anna Sára, Szirtes Botond, Tornyi Napsugár, Túri Zoltán, Urbán István, Vincze Lilla.
5 points:	24 students.
4 points:	9 students.
3 points:	5 students.
2 points:	5 students.
1 point:	14 students.
0 point:	14 students.
Unfair, not evaluated:	8 solutionss.

Problems in Mathematics of KöMaL, October 2016