 |
A K. 635. feladat (2019. november) |
K. 635. Vegyünk egy konkáv négyszöget, és rajzoljuk meg a négyszög belsejében haladó átlóját. Az átló két háromszögre vágja a négyszöget. Igazoljuk, hogy pontosan akkor egyenlő a két háromszög területe, ha ezen átló egyenese felezi a másik átlót.
(6 pont)
A beküldési határidő 2019. december 10-én LEJÁRT.
1. megoldás. Tekintsük az alábbi ábrát:
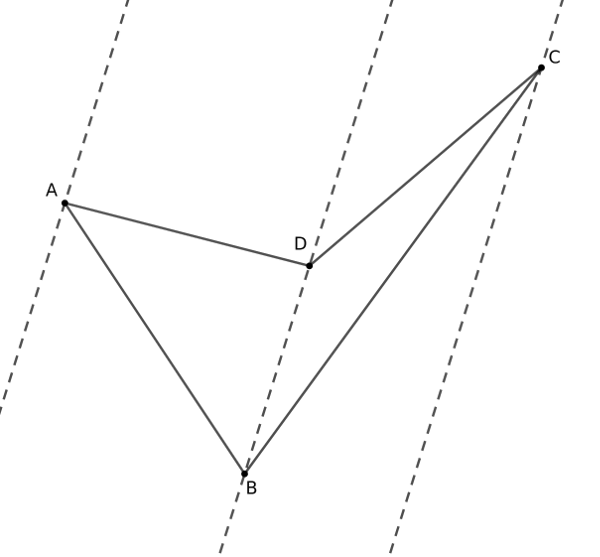
Ha a \(\displaystyle BD\) átló két egyforma területű háromszögre vágja a négyszöget, akkor ezen háromszögek \(\displaystyle BD\)-hez tartozó magasságai megegyeznek. Ez azt jelenti, hogy az \(\displaystyle A\) és \(\displaystyle C\) csúcson keresztül \(\displaystyle BD\)-vel húzott párhuzamosok középpárhuzamosa \(\displaystyle BD\).
Mivel a középpárhuzamos bármely olyan szakaszt felez, mely a párhuzamosok egy-egy pontját köti össze, ezért a \(\displaystyle BD\) egyenes felezi az \(\displaystyle AC\) szakaszt.
Ez az állítás megfordítva is igaz: ha \(\displaystyle BD\) átmegy \(\displaystyle AC\) felezőpontján, akkor a két párhuzamos egyenes középpárhuzamosa, tehát egyenlő távolságra van a két párhuzamostól. Emiatt a két háromszög \(\displaystyle BD\)-hez tartozó magassága megegyezik, vagyis a két háromszög területe is egyenlő.
2. megoldás. Deme Erik (Budapest, Németh László Gimn., 9. o. t.)
Statisztika:
142 dolgozat érkezett. 6 pontot kapott: Cynolter Dorottya, Deme Erik, Hajós Balázs, Kádár 1115 Júlia, Kaltenecker Balázs Bence, Kedves Benedek János, Kiss-Beck Tamara, Slézia Dávid, Vankó Lóránt Albert, Varga 326 Sebestény, Viczián Dániel, Waldhauser Miklós. 5 pontot kapott: Árok Anna, Csintalan Gergely, Somlai Dóra, Tóth Babett. 4 pontot kapott: 7 versenyző. 3 pontot kapott: 43 versenyző. 2 pontot kapott: 15 versenyző. 1 pontot kapott: 11 versenyző. 0 pontot kapott: 39 versenyző. Nem versenyszerű: 4 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 7 dolgozat.
A KöMaL 2019. novemberi matematika feladatai

