 |
A K. 661. feladat (2020. szeptember) |
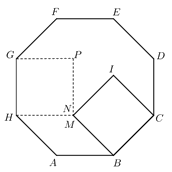
K. 661. Az \(\displaystyle ABCDEFGH\) szabályos nyolcszög 2 egység hosszú \(\displaystyle BC\) és \(\displaystyle GH\) oldalára a \(\displaystyle BCIM\) és a \(\displaystyle GHNP\) négyzetet rajzoljuk befelé. Igazoljuk, hogy az \(\displaystyle N\) és \(\displaystyle M\) pontok egybeesnek.
(6 pont)
A beküldési határidő 2020. október 12-én LEJÁRT.
Megoldás. A szabályos nyolcszög egy belső szöge \(\displaystyle 135^{\circ}\). Mivel \(\displaystyle ABM\angle = 135^{\circ}-90^{\circ}=45^{\circ}=180^{\circ}-135^{\circ}\), ezért \(\displaystyle AH\) és \(\displaystyle BM\) párhuzamosak. Az \(\displaystyle ABMH\) négyszögnek van két párhuzamos és egyenlő hosszú oldala, ezért az \(\displaystyle ABMH\) négyszög paralelogramma. Mivel \(\displaystyle AH = AB = BM = 2\), ezért \(\displaystyle HM = 2\). Mivel az \(\displaystyle ABMH\) paralelogramma minden oldala egyenlő, ezért rombusz, így \(\displaystyle AHM\angle=45^{\circ}\), ahonnan \(\displaystyle GHM\angle= 135^{\circ}-45^{\circ}=90^{\circ}\).
Tehát a \(\displaystyle GH\) és \(\displaystyle HM\) szakaszok egyenlő hosszúak és derékszöget zárnak be, vagyis \(\displaystyle M\) megegyezik a \(\displaystyle GHNP\) négyzet \(\displaystyle N\) csúcsával. Az állítást beláttuk.
Statisztika:
160 dolgozat érkezett. 6 pontot kapott: 79 versenyző. 5 pontot kapott: 10 versenyző. 4 pontot kapott: 7 versenyző. 3 pontot kapott: 16 versenyző. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 13 versenyző. 0 pontot kapott: 21 versenyző. Nem versenyszerű: 1 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 4 dolgozat.
A KöMaL 2020. szeptemberi matematika feladatai

