 |
A K. 731. feladat (2022. szeptember) |
K. 731. Egy \(\displaystyle 4\times6\)-os téglalapot szeretnénk egyrétűen lefedni az ábrán látható L-alakú lappal egybevágó lapokkal. Az L-alakú lapokat tetszés szerint elforgathatjuk, illetve megfordíthatjuk. Van-e legalább 36 különböző lefedés?
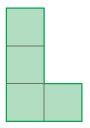
(5 pont)
A beküldési határidő 2022. október 10-én LEJÁRT.
Megoldás. \(\displaystyle 2\times4\)-es téglalapot kétféleképpen lehet lefedni.
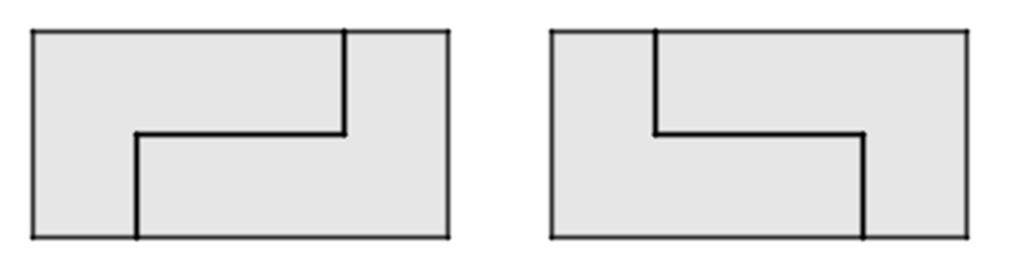
\(\displaystyle 4\times6\)-os téglalapot 3-féleképpen lehet szétbontani \(\displaystyle 2\times4\)-es téglalapra, minden esetben 3 ilyen téglalapot használtunk.
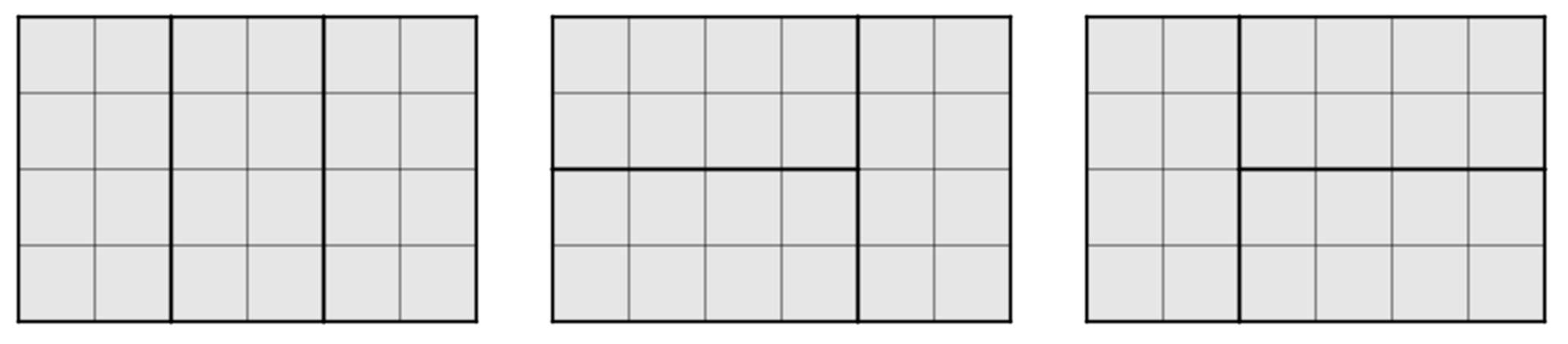
Mindhárom esetben \(\displaystyle 2\cdot2\cdot2=8\) lehetőség van, így összesen 24. (Közöttük azonosak nincsenek.) Például:

\(\displaystyle 4\times4\)-es téglalapot kétféleképpen lehet lefedni (úgy, hogy nem két darab \(\displaystyle 2\times4\)-es téglalapból áll össze).
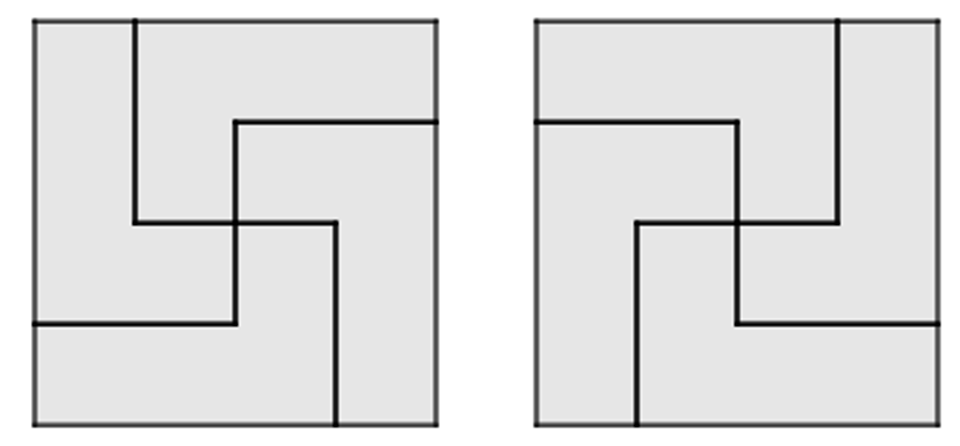
Ezek mellé egy-egy \(\displaystyle 2\times4\)-es téglalapot teszünk (balra, vagy jobbra), így ez is (\(\displaystyle 2\cdot2)\cdot2=8\) lehetőség a lefedésre. Íme a 8 lehetőség egyik fele:

Olyan lefedés is van, amelyik korábban nem szerepelt, ez a négy az egyik \(\displaystyle 4\times4\)-es lefedésből származik és van még négy ilyen a másikból is.

Így összesen 40 lefedést találtunk, tehát van legalább 36 lefedés. (Azt nem bizonyítottuk, hogy nincs több.)
Statisztika:
88 dolgozat érkezett. 5 pontot kapott: Barna 201 Krisztina, Bodor Csanád, Castro Csongor, Csikai Anna Alida, Ébner Jakab, Engi Zita, Farkas Máté, Forrai Boldizsár, Gacsályi Maja, Gárdi Bonifác István, Gyukity Milán, Hajós Boróka, Hodossy-Takács Ráhel, Juhász Noel, Kaposi-Ly Dávid, Kökény Kristóf, Libor Andrea, Mátyus Rebeka, Molnár Lili, Nguyen Minh Kien, Sárecz Bence, Sipos Márton, Stancsics Panna, Stingli Zsuzsanna, Szabó 926 Bálint, Szabó 926 Bence, Szakács Bence Mihály, Szlivka Mihály, Tóth 207 Bence, Zhu Yi. 4 pontot kapott: Balogh Bendegúz, Agárdi Balázs, Bartók Márton, Bartusková Viktória, Eőry Sára , Glavosits Bende, Pulka Gergely Tamás, Tóth Hanga Katalin, Virág Eszter. 3 pontot kapott: 9 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 8 versenyző. Nem versenyszerű: 17 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 5 dolgozat.
A KöMaL 2022. szeptemberi matematika feladatai
