A K. 740. feladat (2022. november)

K. 740. Egy \(\displaystyle 3\times12\)-es téglalapot szeretnénk lefedni 12 db \(\displaystyle 1\times3\)-as téglalappal. Hányféleképpen tehetjük ezt meg?

(5 pont)

A beküldési határidő 2022. december 12-én LEJÁRT.

Megoldás. Ha fekvő \(\displaystyle 1\times3\)-as téglalapot használunk, akkor ezt csak hármasával tehetjük meg, úgy, hogy egyszerre három ilyennel egy \(\displaystyle 3\times3\)-as négyzetnyi részt fedünk le. (Amennyiben nem pontosan egymás fölé helyezzük ezt a három darab fekvő \(\displaystyle 1\times3\)-as téglalapot, hanem valahogyan egymástól elcsúsztatva, akkor a lefedés már nem fejezhető be.)

A fekvő téglalapok száma tehát lehet 0, 3, 6, 9 vagy 12.

Ha nincs fekvő téglalap (mindegyik álló), akkor az 1 lehetőséget ad.

Ha három ilyen téglalap van, akkor ezeket 10-féleképpen helyezhetjük el.

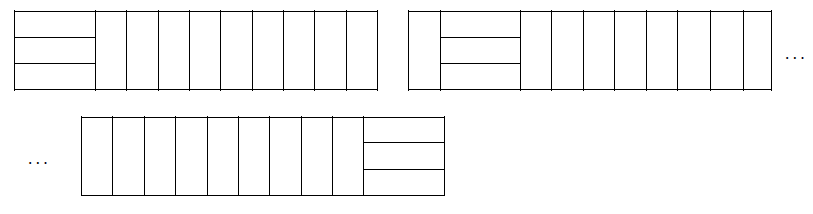
Ha hat ilyen téglalap van, akkor jelöljük a három-három vízszintes téglalapot ,,körbevevő" négyzetek pozícióját a balról számított első oszlopának sorszámával.

A két „keretnégyzet” helyzete lehet: 1-4, 1-5, 1-6, 1-7, 1-8, 1-9, 1-10, továbbá 2-5, 2-6, 2-7, 2-8, 2-9, 2-10, valamint 3-6, 3-7, 3-8, 3-9, 3-10, és így tovább egészen 7-10-ig.

Ez összesen: \(\displaystyle 7+6+5+4+3+2+1=28\) lehetőség.

Ha kilenc ilyen téglalap van, akkor az előzőekhez hasonlóan jelöljük a három-három-három vízszintes téglalapot körbevevő négyzetek pozícióját a balról számított első oszlopának sorszámával.

A három „keretnégyzet” helyzete lehet:
1-4-7, 1-4-8, 1-4-9, 1-4-10 | 1-5-8, 1-5-9, 1-5-10 | 1-6-9, 1-6-10 | 1-7-10 | 2-5-8, 2-5-9, 2-5-10 | 2-6-9, 2-6-10 | 2-7-10 | 3-6-9 , 3-6-10 | 3-7-10 | 4-7-10 |

Ez összesen: \(\displaystyle 20\) lehetőség.

Ha mind a tizenkét téglalap fekvő helyzetű, akkor ezeket 1-féleképpen helyezhetjük el.

Összesen: \(\displaystyle 1+10+28+20+1 = 60\)-féleképpen lehet a téglalapokat elhelyezni.

Statisztika:

84 dolgozat érkezett.
5 pontot kapott:	Barna 201 Krisztina, Bodor Csanád, Budai Máté, Domján István, Ďurčovič Ádám, Horváth Imre, Incze-Nagy Enéh, Kókai Ákos, Kormos Gellért, Kökény Kristóf, Molnár Lili, Nagy Ádám 699, Olláry Samu, Pulka Gergely Tamás, Sipos Márton, Szabó 926 Bálint, Szabó 926 Bence, Szeszler Móric, Sziszkosz Zsófia, Tóth Hanga Katalin.
4 pontot kapott:	Bartusková Viktória, Forrai Eszter , Gyöngyösi Dorottya, Libor Andrea, Móricz Zsombor, Papp Levente, Pikó András, Tajta Sára, Tóth 207 Bence.
3 pontot kapott:	17 versenyző.
2 pontot kapott:	13 versenyző.
1 pontot kapott:	10 versenyző.
0 pontot kapott:	2 versenyző.
Nem versenyszerű:	6 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	7 dolgozat.

A KöMaL 2022. novemberi matematika feladatai