A K. 755. feladat (2023. február)

K. 755. Legfeljebb hány oldala lehet egy olyan konvex sokszögnek, amelynek pontosan 3 tompaszöge van? Adjunk meg egy ilyen sokszöget.

(5 pont)

A beküldési határidő 2023. március 10-én LEJÁRT.

Megoldás. Egy \(\displaystyle n\) oldalú konvex sokszög belső szögeinek összege \(\displaystyle (n - 2) \cdot 180^{\circ}\). A három tompaszög ebből összesen több, mint \(\displaystyle 3 \cdot 90^{\circ}\), de kevesebb, mint \(\displaystyle 3 \cdot180^{\circ}\). A maradék \(\displaystyle n-3\) szög nem tompaszög, tehát egyenként legfeljebb \(\displaystyle 90^{\circ}\)-osak. Azaz \(\displaystyle (n - 2) \cdot 180^{\circ} < 3 \cdot 180^{\circ} + (n - 3) \cdot 90^{\circ}\), amiből \(\displaystyle 2(n - 2) < n -3 + 6\), azaz \(\displaystyle n < 7\), tehát legfeljebb hat oldalú lehet a sokszög.

Ilyen konvex hatszögek valóban léteznek, ahogy azt az alábbi ábra két hatszöge mutatja.

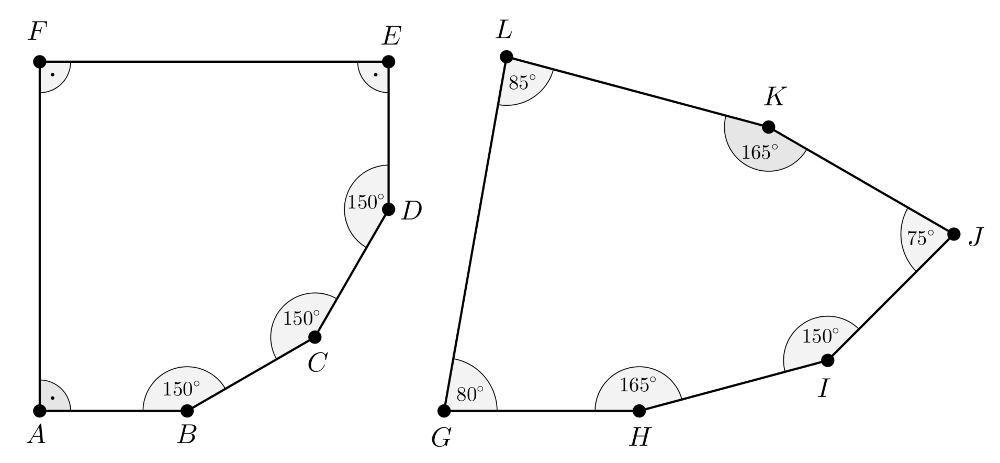
Az \(\displaystyle ABCDE\) hatszög szögeinek nagysága rendre

\(\displaystyle 90^{\circ}, 150^{\circ}, 150^{\circ}, 150^{\circ}, 90^{\circ},\)

míg a \(\displaystyle GHIJKL\) hatszög szögeinek mértéke rendre

\(\displaystyle 80^{\circ}, 165^{\circ}, 150^{\circ}, 75^{\circ}, 165^{\circ}, 85^{\circ}.\)

Mindkét hatszög eleget tesz a feladat minden feltételének.

Statisztika:

A K. 755. feladat értékelése még nem fejeződött be.

A KöMaL 2023. februári matematika feladatai