 |
A K. 765. feladat (2023. április) |
K. 765. Az \(\displaystyle ABC\) háromszög \(\displaystyle AB\) oldalának felezőpontja \(\displaystyle D\), a \(\displaystyle CD\) szakasz felezőpontja \(\displaystyle E\). Hol kell felvenni a \(\displaystyle CD\) szakaszon az \(\displaystyle F\) pontot, hogy az \(\displaystyle AEC\) és \(\displaystyle BFC\) háromszögek területének összege az \(\displaystyle ABC\) háromszög területének pontosan \(\displaystyle 40\%\)-a legyen?
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2023. május 10-én LEJÁRT.
Megoldás. Tekintsük az alábbi ábrát.
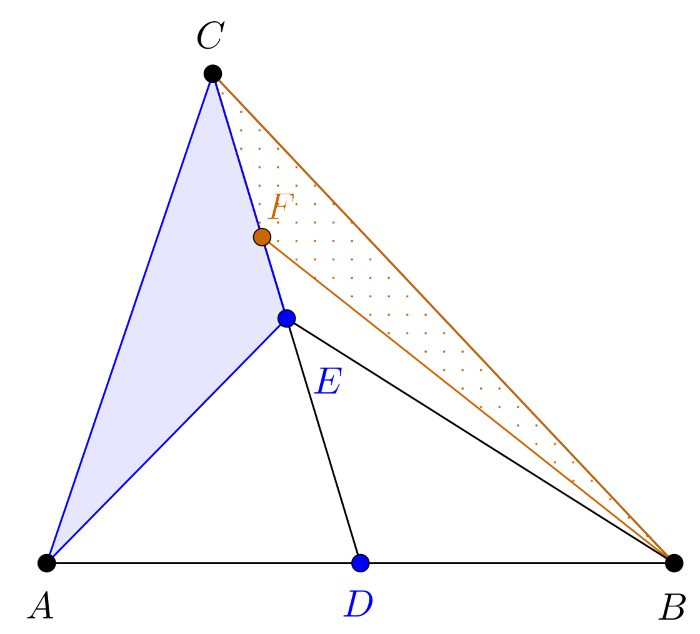
Ismert, hogy a háromszög súlyvonala felezi a háromszög területét, ezért a \(\displaystyle CD\) súlyvonal által létrehozott \(\displaystyle ADC\) háromszög területe éppen fele az \(\displaystyle ABC\) háromszög területének.
Ugyanakkor az \(\displaystyle AE\) szakasz súlyvonala az \(\displaystyle ADC\) háromszögnek, tehát \(\displaystyle AE\) felezi az \(\displaystyle ADC\) háromszög területét. Ebből azonnal következik, hogy
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{T_{AEC}=\frac{T_{ABC}}{4}}.\) |
A feladat feltétele szerint:
\(\displaystyle \displaystyle{T_{AEC}+T_{FBC}=0,4\cdot T_{ABC}},\)
ahonnan (1) felhasználásával kapjuk, hogy
\(\displaystyle \displaystyle{0,25\cdot T_{ABC}+T_{FBC}=0,4\cdot T_{ABC}},\)
azaz
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{T_{FBC}=0,15\cdot T_{ABC}}.\) |
A \(\displaystyle CFB\) és a \(\displaystyle CDB\) háromszögek \(\displaystyle B\) csúcshoz tartozó magassága egyenlő, ezért területeikre igaz, hogy:
| \(\displaystyle (3)\) | \(\displaystyle \frac{CF}{CD}=\frac{T_{FBC}}{T_{CDB}}=\frac{0,15\cdot T_{ABC}}{0,5\cdot T_{ABC}}=\frac{3}{10}.\) |
A kapott eredmény azt jelenti, hogy az \(\displaystyle F\) pontot a \(\displaystyle CD\) szakaszon a \(\displaystyle C\)-től számított harmadik tizedelőpontban kell felvenni, és (3)-ból az is világosan látszik, hogy ez az \(\displaystyle F\) pont megfelel a feladat azon feltételének, hogy a \(\displaystyle CD\) szakasz belső pontja legyen.
Statisztika:
42 dolgozat érkezett. 5 pontot kapott: Agárdi Balázs, Derűs Ádám , Domján István, Horváth Imre, Juhász Noel, Kókai Ákos, Kökény Kristóf, Libor Andrea, Lukács Ármin, Móricz Zsombor, Pulka Gergely Tamás, Tajta Sára, Tóth Hanga Katalin. 4 pontot kapott: Bartusková Viktória, Hodossy-Takács Ráhel, Labádi Balázs, Mixtay Marcell, Molnár Lili, Tóth 207 Bence, Valánszki Bulcsú. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 8 versenyző. Nem versenyszerű: 5 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2023. áprilisi matematika feladatai
