 Problem K. 830. (November 2024)
Problem K. 830. (November 2024)
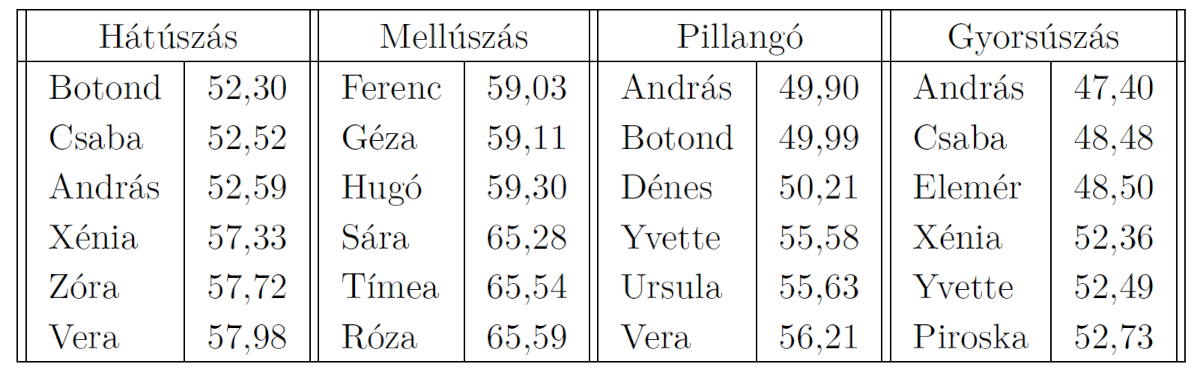
K. 830. In swimming competitions, there are mixed-gender 4x100 m medley relay races. This means that the team consists of two men and two women, and in each stroke 100 meters has to be completed. It's up to the team to decide which stroke the male and female members will compete in. The best times achieved by the swimmers for the 100-meter segments is the following. In backstroke Botond 52.30; Csaba 52.52; András 52.59; Xénia 57.33; Zóra 57.72; Vera 57.98. In breaststroke Ferenc 59.03; Géza 59.11; Hugó 59.30; Sára 65.28; Tímea 65.54; Róza 65.59. In butterfly András 49.90; Botond 49.99; Dénes 50.21; Yvette 55.58; Ursula 55.63; Vera 56.21. In freestyle stroke András 47.40; Csaba 48.48; Elemér 48.50; Xénia 52.36; Yvette 52.49; Piroska 52.73. Supposing that the swimmers can achieve the same results in a competition, find the composition of the team that provides the best possible result.
(5 pont)
Deadline expired on December 10, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az elvileg elérhető leggyorsabb csapat akkor jön ki, ha a legjobb időeredményeket hasonlítjuk össze a férfiak és a nők esetében, és úgy választjuk ki a két női csapattagot és úszásnemet hozzájuk, hogy a férfiak eredményéhez a legkisebb plusz idő adódjon hozzá. (A táblázatban látható, hogy a legjobb három férfi minden úszásnemben gyorsabb, mint a legjobb három nő). A táblázat alapján a hátúszásban +5,03 mp, a mellúszásban +6,25 mp, a pillangóban +5,68 mp, a gyorsúszásban +4,96 mp az eltérés az első helyek között. A leggyorsabbak tehát akkor lennének, ha a gyorsúszásban és a hátúszásban szerepelne a legjobb nő, a másik kettőben pedig a legjobb férfi. Ez viszont nem valósítható meg, hiszen Xénia csak egyszer úszhat. Látható továbbá, hogy a mellúszó választása nem befolyásolja a többi úszásnemet, így ott a különbség a férfi-nő csere esetén mindig ugyanannyi.
Két esetet kell tehát megvizsgálnunk:
1. eset. Gyorsúszásban Xénia megy (+4,96 mp). Ekkor ha megy a pillangón, akkor az +5,68 mp, ha Zóra megy a hátúszásban, az +5,42 mp, tehát ebben az esetben Zóra beállítása gyorsabb csapatot ad (+4,96+5,42 = +10,38 mp). A férfi mellúszót ebben az esetben nem érdemes cserélni.
2. eset. Xénia hátúszásban megy (+5,03 mp). Ha Yvette megy pillangón, akkor az +5,68 mp, ha Yvette gyorsúszásban megy, akkor az +5,29 mp, tehát ebben az esetben Yvette a gyorsúszással gyorsabb csapatot ad (+5,03+5,29 = +10,32 mp), és a férfi mellúszót ebben az esetben sem érdemes cserélni. Ez jobb idő, mint az 1. esetben kapott csapat, így ezt az összeállítást kell választani: Xénia hát, Ferenc mell, András pillangó és Yvette gyors.
Megjegyzés. Az úgynevezett mohó algoritmus (minden lépésben válasszuk a lehető legjobbat) az 1. esetnek megfelelő csapatot adná, ami láthatóan nem a legjobb. Ezért kell körültekintően mérlegelni a választási lehetőségeket több lépésre előre figyelve.
Statistics:
114 students sent a solution. 5 points: Abonyi Gábor, Chen Zhibo, Császi Balázs, Csehi Panna, Csík Zoltán Richárd, Fülöp Balázs, Győrffy Csanád, Hajdu Vince, Hollósi Dominik, Imolya Mirella Petra, Izsa Ferenc Gergő, Jancsurák Flóra, Kaj Huba Csaba, Lukács Luca, Medgyesi András, Rácz Koppány Bendeguz, Rózsa Péter, Söderberg Kajsa. 4 points: 40 students. 3 points: 17 students. 2 points: 9 students. 1 point: 8 students. 0 point: 12 students. Not shown because of missing birth date or parental permission: 10 solutions.
Problems in Mathematics of KöMaL, November 2024
