Problem K. 846. (February 2025)

K. 846. The LIGO company’s new building toy consists of identical building blocks. Each building block consists of four glued-together small cubes with 2 cm edges. What is the maximum number of building blocks that can fit into a box with dimensions \(\displaystyle 6~\mathrm{cm}\times 6~\mathrm{cm}\times 8~\mathrm{cm}\)?

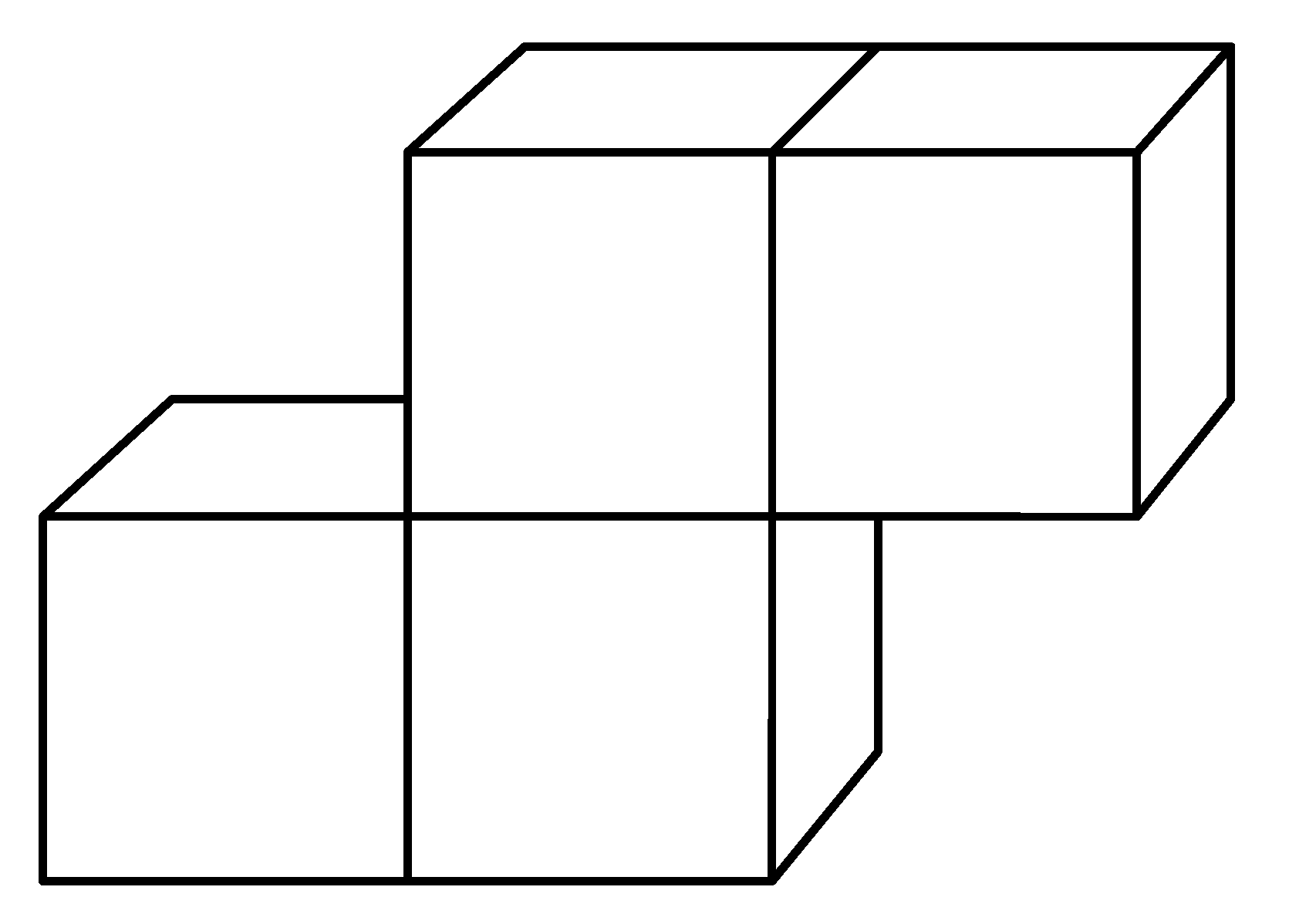
(5 pont)

Deadline expired on March 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A 6 cm \(\displaystyle \times\) 6 cm \(\displaystyle \times\) 8 cm méretű dobozba \(\displaystyle 3 \cdot 3 \cdot 4 = 36\) darab 2 cm \(\displaystyle \times\) 2 cm \(\displaystyle \times\) 2 cm méretű kiskocka fér, azaz legfeljebb \(\displaystyle (36 : 4 =) 9\) darab építőelem.

Nyolc építőelem elhelyezhető, kilenc nem.

Színezzük a 36 kockát oszloposan pepitára (Lásd az ábrát.) Egy ilyen kockarácsba akárhogyan helyezünk el egy építőelemet, összességében 2 sötét és 2 világos kocka helyét foglalja el. Mivel 4-gyel több sötét kiskocka van, mint világos, így legfeljebb 8 építőelem helyezhető el a dobozban. Ez meg is valósítható az alábbi ábra alapján, melyben az első két rétegben helyeztünk el 4 építőelemet és ugyanígy a felső két rétegben újabb négy elhelyezhető.

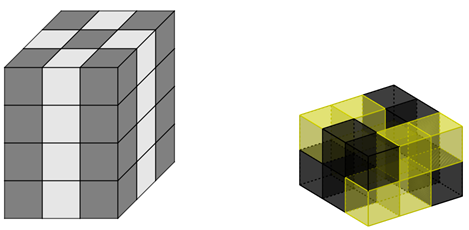
Statistics:

88 students sent a solution.
5 points:	Csík Zoltán Richárd, Lovas Márk, Patócs 420 Péter.
4 points:	Kudomrák Lili Anna , Laczó Zoltán, Molnár Levente, Rózsa Péter, Szabados Ákos, Zsilák Márk Péter.
3 points:	5 students.
2 points:	16 students.
1 point:	20 students.
0 point:	29 students.
Not shown because of missing birth date or parental permission:	9 solutions.

Problems in Mathematics of KöMaL, February 2025