Problem K. 849. (March 2025)

K. 849. Find the smallest number of matches that can be removed in the figure such that no square remains.

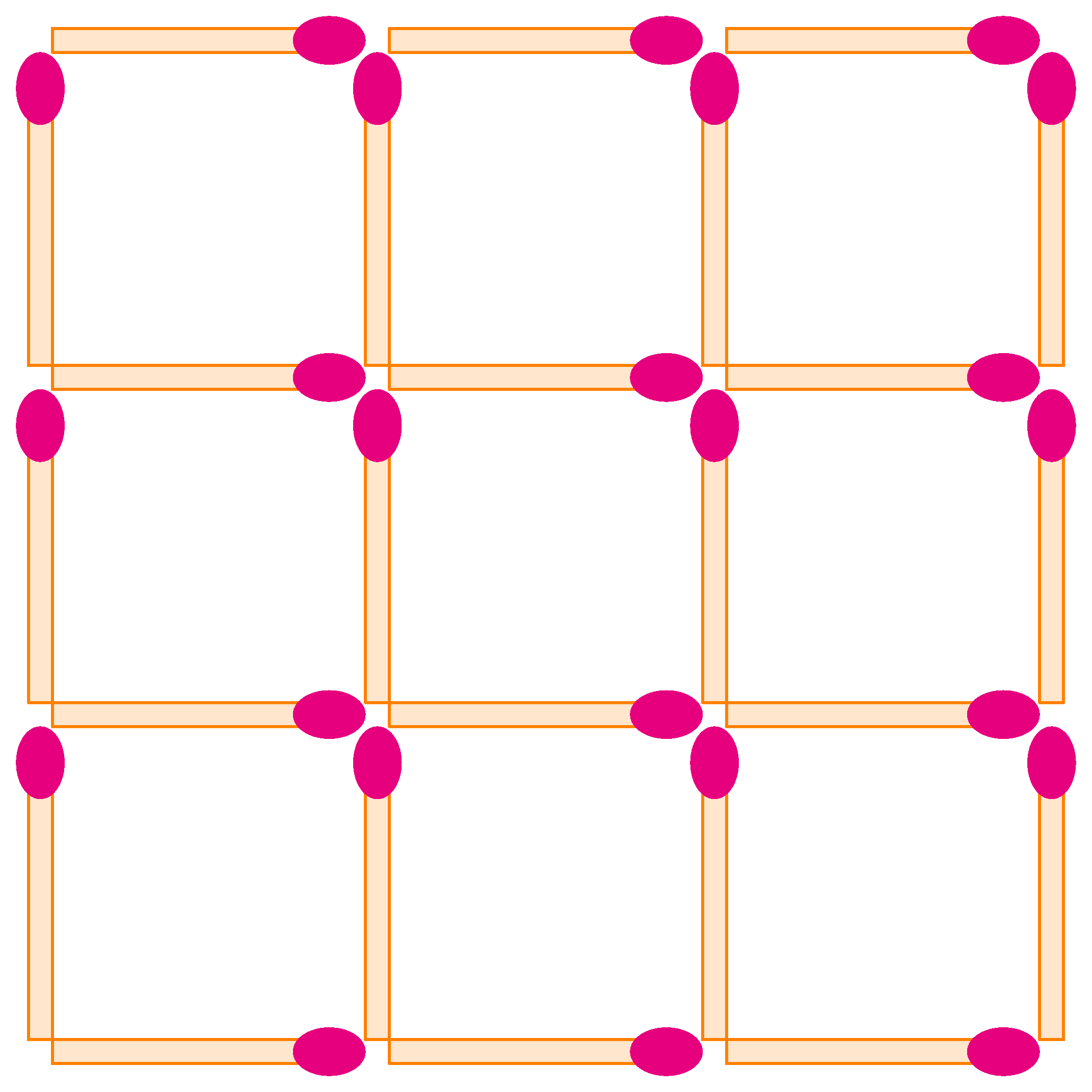
(5 pont)

Deadline expired on April 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Ha csak a kis négyzeteket szeretnénk megszüntetni, akkor ehhez legalább öt gyufa elvétele szükséges, mert egy gyufa legfeljebb két kis négyzethez tartozhat.

A négy darab \(\displaystyle 2\times2\)-es négyzet megszüntetéséhez két gyufa elvétele elegendő, mert a gyufasorok, illetve gyufaoszlopok közepén lévő gyufák két-két ilyen négyzethez is tartoznak.

A legnagyobb négyzet megszüntetéséhez el kell venni egy gyufát az ábra külső 12 gyufája közül.

Öt gyufa elvétele nem elég. Egy biztosan a külső gyufák közül való (a nagy négyzet miatt). A kerületről elvett gyufa által megszűnt kis négyzeten kívül 8 darab kis négyzetet kell páronként egy-egy gyufa elvételével megszüntetni.

Ha az oldal egyik középső gyufáját vesszük el, akkor nem is lehet párosával megszüntetni a megmaradó 8 kis négyzetet (Lásd ábra!).

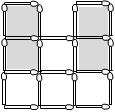
Ha az oldal egyik szélső gyufáját vesszük el, akkor végignézve a lehetőségeket mindegyik esetben marad egy-egy \(\displaystyle 2\times2\)-es négyzet. (Lásd ábra.)

Hat gyufa elvételével megoldható. Pl:

Statistics:

97 students sent a solution.
5 points:	Csík Zoltán Richárd, Holló Barnabás, Izsa Ferenc Gergő, Laczó Zoltán, Lovas Márk, Medgyesi András, Nagy Alexander, Patócs 420 Péter, Rózsa Péter.
4 points:	Bloemsma Péter Sándor, Kudomrák Lili Anna , Mátyás Levente, Molnár Levente.
3 points:	6 students.
2 points:	12 students.
1 point:	32 students.
0 point:	23 students.
Unfair, not evaluated:	5 solutionss.
Not shown because of missing birth date or parental permission:	6 solutions.

Problems in Mathematics of KöMaL, March 2025