Problem K. 855. (April 2025)

K. 855. Three ships left the dock at the same time. One ship was travelling north, and the other two were travelling southeast. All three ships arrived at their first stop at the same exact time. The pair travelling in the same direction split up, one of them kept travelling southeast, but the other one started in the direction of the third ship that was stationary at its first stop. Once again, they've reached their destination at the same exact time. In what direction should the two ships being at the same place travel to reach the second destination of the ship that was travelling southeast all along?

Proposed by: Katalin Abigél Kozma, Győr

(5 pont)

Deadline expired on May 12, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Készítsünk ábrát a szöveg alapján! A hajók a \(\displaystyle K\) pontból indulnak, az északi kikötő helyét \(\displaystyle L\), a délkeleti irányban lévő kikötők helyét \(\displaystyle M\), illetve \(\displaystyle N\) pont jelöli. Feladatunk, hogy az ábrán \(\displaystyle \varphi\)-vel jelölt \(\displaystyle NLK \sphericalangle\) szög nagyságát meghatározzuk.

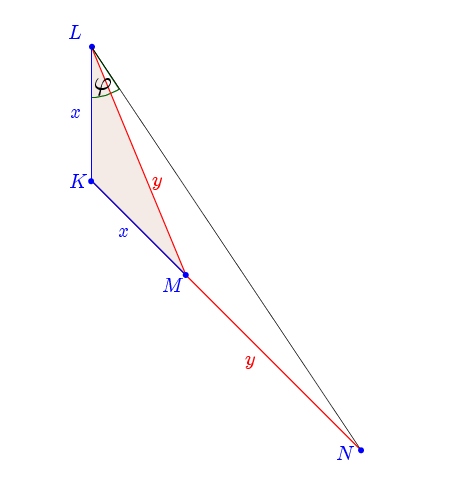
Ekkor az északi és a délkeleti irány miatt \(\displaystyle LKM \sphericalangle=135^\text{\(\displaystyle \circ\)}.\) Az egy időben való érkezés és az azonos átlagsebesség miatt \(\displaystyle KL=KM\), illetve \(\displaystyle ML=MN\), ezen szakaszok hosszát \(\displaystyle x\)-szel, illetve \(\displaystyle y\)-nal jelöltük. Nyilvánvaló, hogy az \(\displaystyle LKM\) és az \(\displaystyle LMN\) háromszög is egyenlő szárú. Először az \(\displaystyle LKM\) háromszög alapon fekvő szögeit tudjuk kiszámolni:

\(\displaystyle MLK \sphericalangle=KML \sphericalangle=\frac{180^\text{\(\displaystyle \circ\)}-135^\text{\(\displaystyle \circ\)}}{2}=22,\!5^\text{\(\displaystyle \circ\)}.\)

A \(\displaystyle KML\sphericalangle\) külső szöge az \(\displaystyle LMN\) háromszögnek, így nagysága egyenlő a nem mellette fekvő két belső szög összegével, ezért

\(\displaystyle NLM \sphericalangle=MNL \sphericalangle=\frac{22,\!5^\text{\(\displaystyle \circ\)}}{2}=11,\!25^\text{\(\displaystyle \circ\)}.\)

A \(\displaystyle \varphi\) szög az \(\displaystyle MLK \sphericalangle\) és az \(\displaystyle NLM \sphericalangle\) összege, így a keresett szög mértéke:

\(\displaystyle \varphi=22,\!5^\text{\(\displaystyle \circ\)}+11,\!25^\text{\(\displaystyle \circ\)}=33,\!75^\text{\(\displaystyle \circ\)}.\)

A két hajó az északi irányhoz, tehát a \(\displaystyle \overrightarrow{KL}\) vektor irányához képest az \(\displaystyle \overrightarrow{LN}\) irányban halad az \(\displaystyle N\) kikötő felé, a két vektor irányának bezárt szöge \(\displaystyle 180^{\circ}-33,75^{\circ}=146,25^{\circ}\), ezért az északi irányhoz képest \(\displaystyle 146,25^{\circ}\)-os szögben kell elindulniuk.

Statistics:

70 students sent a solution.
5 points:	Barta Zsófia, Bloemsma Péter Sándor, Chen Zhibo, Csík Zoltán Richárd, Felföldi Zsófia, Fülöp Balázs, Hajdu Vince, Holló Barnabás, Hollósi Dominik, Izsa Ferenc Gergő, Jancsurák Flóra, Kása Richárd Zsolt, Kovács Domonkos, Kudomrák Lili Anna , Lovas Márk, Macskássy Márk, Majer Veronika, Máté Zsófia, Molnár Levente, Mosonyi Mátyás, Nagy Alexander, Patócs 420 Péter, Péter Tamás, Pocsay Bence Máté, Radošická Emma, Rózsa Péter, Scott Elizabeth, Szabó Balázs, Szabó Milos Farkas, Szighardt Anna, Zsilák Márk Péter.
4 points:	Balla Botond, Elekes Emma, Forinyák Anna Vanda, Fórján Bernát, Gintner Annabella , Győrffy Csanád, Havasi Huba László, Havasi Máté Pál, Kun Milán, Laczó Zoltán, Lukács Luca, Makra Zóra Liliána, Máthé Csongor Örs, Medgyesi András, Némethy Márk, Raschek Vince, Silye Zalán, Szabó Szilárd, Tóth Emma Luca.
3 points:	2 students.
2 points:	2 students.
1 point:	5 students.
0 point:	4 students.
Not shown because of missing birth date or parental permission:	7 solutions.

Problems in Mathematics of KöMaL, April 2025