 |
A P. 4603. feladat (2014. január) |
P. 4603. Számítsuk ki az ábrán látható, mindkét irányban végtelen, csupa R ellenállásból álló láncban az alábbi pontok közötti eredő ellenállást:
a) A és B;
b) A és C!
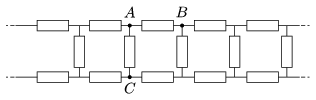
Közli: Cserti József, Budapest
(5 pont)
A beküldési határidő 2014. február 10-én LEJÁRT.
Megoldásvázlat. a)
b)
Statisztika:
63 dolgozat érkezett. 5 pontot kapott: Antalicz Balázs, Asztalos Bogdán, Balogh Menyhért, Bencsik Bálint, Bereczki Zoltán, Blum Balázs, Bugár 123 Dávid, Büki Máté, Csathó Botond, Csordás Gábor, Di Giovanni Márk, Dinev Georgi, Fehér Zsombor, Fekete Panna, Forrai Botond, Holczer András, Horicsányi Attila, Hornyák Szabolcs, Hoyle Anna, Iván Balázs, Janzer Barnabás, Juhász Péter, Kaposvári Péter, Kasza Bence, Kovács Péter Tamás, Körei Réka Enikő, Mándoki László, Morvay Bálint, Németh Gergely, Olosz Balázs, Öreg Botond, Sal Kristóf, Seress Dániel, Szász Norbert Csaba, Szentivánszki Soma , Szépfalvi Bálint, Szirbik Bence, Tóth Bence Tamás, Trócsányi Péter, Verasztó Ádám, Virágh Anna, Wiandt Péter, Zarándy Álmos. 4 pontot kapott: Csernák Tamás, Gróf Tamás, Kaszás Bálint, Németh 017 András, Rózsa Tibor, Szathmári Balázs, Szilágyi András. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2014. januári fizika feladatai
