A P. 4643. feladat (2014. május)

P. 4643. Egy vízszintes, vékony cső mindkét vége zárt. A cső közepén egy $\displaystyle h$ hosszúságú higanyszál van. A levegőoszlopok hossza mindkét térrészben $\displaystyle \ell$, a nyomás mindkét oldalon $\displaystyle H$ magasságú higanyoszlop hidrosztatikai nyomásával egyenlő. A csövet egy függőleges tengelyű centrifugagépre helyezzük, és $\displaystyle \omega$ szögsebességgel megforgatjuk.

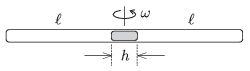
Mekkora periódusidejű (kis) rezgéseket végezhet a higanyszál, ha a hőmérséklet állandó? Feltételezhetjük, hogy $\displaystyle \ell$-hez képest $\displaystyle h$ viszonylag kicsi, emiatt a higanyszál nem szakad el. (Lásd még a P. 4609. feladat megoldását lapunk 309. oldalán!)

Varga István (1952-2007) feladata

(5 pont)

A beküldési határidő 2014. június 10-én LEJÁRT.

Megoldásvázlat. Ha $\displaystyle \omega<\omega_\text{krit.}=\sqrt{\frac{2gH}{\ell h}},$ akkor

$\displaystyle T=2\pi\sqrt{\frac{1}{\omega_\text{krit.}^2-\omega^2}},$

ha viszont $\displaystyle \omega>\omega_\text{krit.}$, úgy a rezgésidő

$\displaystyle T=2\pi \frac{\omega_\text{krit.}}{\omega}\sqrt{\frac{1}{2 ( \omega^2-\omega_\text{krit.}^2)}}.$

Statisztika:

23 dolgozat érkezett.
5 pontot kapott:	Berta Dénes, Fehér Zsombor, Fekete Panna, Holczer András, Horicsányi Attila, Janzer Barnabás.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	3 versenyző.

A KöMaL 2014. májusi fizika feladatai