A P. 4644. feladat (2014. május)

P. 4644. Fürdőszobai falunkra \(\displaystyle r=55\) mm sugarú papírtekercset rögzítünk. A tekercset egy csuklós drótkeret tartja, amelynek két csuklója azonos magasságban, a faltól \(\displaystyle d=15\) mm távolságra helyezkedik el. A keret két oldalsó darabja \(\displaystyle \ell=90\) mm hosszúságú, ez egyben a csuklók távolsága a papírhenger tengelyétől. A papírtekercs elhanyagolható súrlódással forgatható el a keret középső darabja körül. Nyugalmi állapotban a szerkezet a súlya folytán a falhoz támaszkodik. A papír és a falicsempe közötti súrlódási együttható \(\displaystyle \mu=0{,}2\).

A papír végét állandó sebességgel lefelé húzzuk.

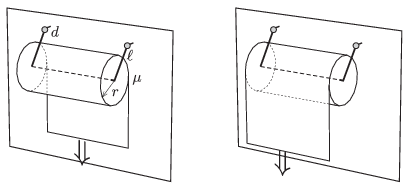
\(\displaystyle a)\) Melyik esetben kell ehhez nagyobb erőt kifejtenünk, ha a papír szabad vége a tekercs fal felőli oldalán, vagy pedig ha a faltól távolabbi oldalán van?

\(\displaystyle b)\) Mekkora a két erő aránya?

\(\displaystyle c)\) Mekkora ez az arány, ha a papírtekercs sugara \(\displaystyle r=100\) mm?

Közli: Kós Géza, Budapest

(5 pont)

A beküldési határidő 2014. június 10-én LEJÁRT.

Megoldásvázlat. \(\displaystyle a)\) A faltól távolabbi oldalon nagyobb (\(\displaystyle F_2\)) erőt kell kifejteni, mint a másik oldalon (\(\displaystyle F_1\)).

\(\displaystyle b)\) \(\displaystyle \frac{F_2}{F_1}=\frac{1}{1-2\mu\,{\rm tg} \alpha}\approx 1{,}25\), ahol \(\displaystyle \sin\alpha=\frac{r-d}{\ell}\).

\(\displaystyle c)\) Ha \(\displaystyle r\rightarrow 98,6\) mm, \(\displaystyle F_2/F_1\rightarrow\infty\), ilyenkor a papír végét nem lehet egyenletes sebességgel lefelé húzni, a papír elszakad.

Statisztika:

34 dolgozat érkezett.
5 pontot kapott:	Antalicz Balázs, Asztalos Bogdán, Balogh Menyhért, Berta Dénes, Blum Balázs, Csathó Botond, Farkas Tamás, Fehér Zsombor, Fekete Panna, Forrai Botond, Holczer András, Horicsányi Attila, Kaposvári Péter, Kasza Bence, Kormányos Hanna Rebeka, Kovács Péter Tamás, Krokos Ádám László, Olosz Balázs, Öreg Botond, Rózsa Tibor, Sal Kristóf, Sárvári Péter, Trócsányi Péter, Varju Ákos.
4 pontot kapott:	Bugár 123 Dávid, Büki Máté, Morvay Bálint, Pázmán Zalán, Szász Norbert Csaba, Szépfalvi Bálint.
3 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2014. májusi fizika feladatai