 |
A P. 4686. feladat (2014. december) |
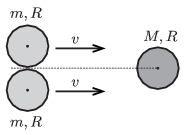
P. 4686. Vízszintes, légpárnás asztalon két egyforma, \(\displaystyle m\) tömegű, \(\displaystyle R\) sugarú korong egymással érintkezve, a középpontjaikat összekötő irányra merőlegesen, azonos \(\displaystyle v\) sebességgel mozog. A középpontjaikat összekötő szakasz felezőmerőlegesén helyezkedik el egy harmadik, \(\displaystyle M\) tömegű, \(\displaystyle R\) sugarú nyugvó korong középpontja. A mozgó korongok tökéletesen rugalmasan ütköznek a nyugvóval. Ütközés közben a korongok pereme közt sincs súrlódás.
\(\displaystyle a)\) \(\displaystyle M=m\) esetén mekkora lesz az ütközés után a korongok sebességének nagysága és milyen az iránya?
\(\displaystyle b)\) Mekkora \(\displaystyle M/m\) tömegarány esetén mozognak a \(\displaystyle m\) tömegű korongok eredeti sebességük irányára merőlegesen?
Közli: Zsigri Ferenc, Budapest
(5 pont)
A beküldési határidő 2015. január 12-én LEJÁRT.
Megoldás: \(\displaystyle a)\) A kezdetben mozgó korongok sebessége az ütközés után az eredeti mozgásirányban \(\displaystyle 2v/5\), arra merőlegesen \(\displaystyle \pm \sqrt{3}v/{5}\). Ezen vektorok nagysága kb. \(\displaystyle 0{,}76\,v\), irányuk az eredeti mozgásiránnyal kb. \(\displaystyle 41^\circ\)-os szöget zár be. A meglökött korong sebessége \(\displaystyle 6v/5\) lesz.
\(\displaystyle b)\) \(\displaystyle M=3m\) esetén a kisebb tömegű korongok merőleges irányban \(\displaystyle \pm v/\sqrt{3}\) sebességgel pattannak el egymástól, a nagyobb tömegű korong pedig a szimmetriatengely mentén \(\displaystyle 2v/3\) sebességgel fog mozogni.
Statisztika:
42 dolgozat érkezett. 5 pontot kapott: Asztalos Bogdán, Balogh Menyhért, Berta Dénes, Blum Balázs, Bugár 123 Dávid, Csathó Botond, Csorba Benjámin, Di Giovanni Márk, Fehér Balázs, Fekete Panna, Forrai Botond, Fülöp Erik, Gróf Tamás, Holczer András, Iván Balázs, Kaposvári Péter, Kormányos Hanna Rebeka, Kovács Péter Tamás, Körmöczi Dávid, Körtefái Dóra, Marosvári Kristóf, Németh Flóra Boróka, Olosz Balázs, Páhoki Tamás, Sal Kristóf, Szántó Benedek, Szász Norbert Csaba, Szentivánszki Soma , Trócsányi Péter. 4 pontot kapott: Varju Ákos, Wiandt Péter. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2014. decemberi fizika feladatai
