 |
A P. 4767. feladat (2015. október) |
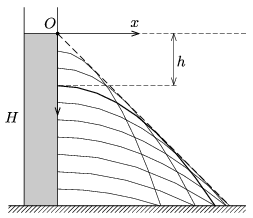
P. 4767. Egy függőleges tengelyű mérőhenger falába sok apró lyukat fúrtunk. A hengert \(\displaystyle H\) magasságig feltöltjük vízzel, melynek következtében a lyukakon (a mérőhenger falára merőlegesen) vékony vízsugarak lövellnek ki. Milyen alakú a vízsugarak burkolófelülete? (A vízsugarak nem akadályozzák egymást, és folyamatos utántöltéssel gondoskodunk a hengerben a vízszint állandóságáról.)
Közli: Vigh Máté, Budapest (Kunfalvi Rezső olimpiai válogatóverseny, 2015)
(6 pont)
A beküldési határidő 2015. november 10-én LEJÁRT.
Megoldás. Tekintsünk egy olyan vízsugarat, amely a vízfelszin alatt \(\displaystyle h\) mélységben található kis lyukon lövell ki. A Torricelli-törvény szerint a kiáramlás sebessége \(\displaystyle \sqrt{2gh}\), a vízsugár alakját megadó függvény pedig (az ábrán látható koordináta-rendszerben) a vízszintes hajítás képleteinek megfelelően
| (1) | \(\displaystyle y(x)=\frac{x^2}{4h}+h.\) |
Egy \(\displaystyle (x,y)\) koordinátákkal megadott pontba csak akkor juthat el valamelyik vízsugár, ha az (1) egyenlet átrendezéséből kapható
| (2) | \(\displaystyle 4h^2-4hy +x^2=0,\) |
\(\displaystyle h\)-ra nézve másodfokú egyenletnek valós gyökei vannak. Ennek az a feltétele, hogy a diszkrimináns nemnegatív:
\(\displaystyle 16y^2-16x^2\geq0.\)
Ez az \(\displaystyle y\geq x \) egyenlőtlenséggel egyenértékű, hiszen a fizikailag reális tartományban \(\displaystyle x>0\) és \(\displaystyle y>0\).
A vízsugarak burkolófelülete tehát egy olyan csonkakúp, amelynek alkotói \(\displaystyle 45^\circ\)-os szöget zárnak be a vízszintessel, felső körlapja pedig éppen a víz felszínének magasságában van.
Statisztika:
59 dolgozat érkezett. 6 pontot kapott: Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Bencsik Bálint, Blum Balázs, Csenger Géza, Di Giovanni András, Édes Lili, Fehér 169 Szilveszter, Fekete Balázs Attila, Forrai Botond, Ghada Alshalan, Hamza Mohammed Almalki, Iván Balázs, Jeges Viktor, Juhász 326 Dániel, Kádár 012 István, Kasza Bence, Klász Viktória, Kormányos Hanna Rebeka, Kovács Péter Tamás, Mány Bence, Marozsák Tóbiás , Nagy Kartal, Olosz Adél, Páhoki Tamás, Pszota Máté, Sal Kristóf, Szemerédi Levente, Szentivánszki Soma , Szépfalvi Bálint, Tomcsányi Gergely, Tompa Tamás Lajos, Tóth Adrián, Varga-Umbrich Eszter, Vígh Márton, Virág Barnabás, Zalavári Márton. 5 pontot kapott: Bartók Imre, Büki Máté. 4 pontot kapott: 3 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 5 dolgozat.
A KöMaL 2015. októberi fizika feladatai
