 |
A P. 4773. feladat (2015. november) |
P. 4773. Egy \(\displaystyle L=2\) m hosszú homogén, vékony rúd egyik végével mennyezeti kampóra van felakasztva. A rudat a vízszintesig kitérítjük, majd kezdősebesség nélkül elengedjük. Amikor átlendülve függőleges helyzetén a függőlegessel \(\displaystyle 30^\circ\)-os szöget zár be a rúd, a kampóról leválik.
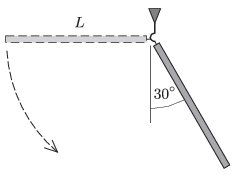
\(\displaystyle a)\) Legalább milyen mélyen van a talaj a kampótól mérve, ha a rúd függőleges helyzetben érkezik a talajra?
\(\displaystyle b)\) Legfeljebb milyen magasra jut mozgása során a rúd alsó végpontja?
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2015. december 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Az energiamegmaradás tételét alkalmazva megkaphatjuk, hogy a rúd leválásának pillanatában a rúd szögsebessége 3,57 \(\displaystyle {\rm s} ^{-1}\), tömegközéppontjának sebessége 3,57 m/s. A mozgás további részében a rúd egyenletesen forog, tömegközéppontja pedig egy ferde hajításnak megfelelő mozgást végez.
A talaj legalább
\(\displaystyle \frac{L}2 \left( \frac{25 \pi^2}{108\sqrt3}-\frac{5\pi}{12}+1+\frac{\sqrt3}{2} \right)=3{,}2~{\rm m}\)
mélyen van a kampó alatt.
\(\displaystyle b)\) Az alsó végpont legmagasabb helyzetében 0,52 m-rel van a kampó szintje alatt.
Statisztika:
59 dolgozat érkezett. 5 pontot kapott: Asztalos Bogdán, Bartók Imre, Blum Balázs, Büki Máté, Csenger Géza, Csire Roland, Csorba Benjámin, Di Giovanni András, Fehér 169 Szilveszter, Forrai Botond, Iván Balázs, Jakus Balázs István, Kasza Bence, Kovács Péter Tamás, Körmöczi Dávid, Olosz Adél, Sal Kristóf, Szentivánszki Soma , Takács Attila, Tófalusi Ádám. 4 pontot kapott: Édes Lili, Ghada Alshalan, Hanusz Fruzsina, Németh 777 Róbert, Németh Flóra Boróka, Páhoki Tamás, Pataki 245 Attila, Pázmán Előd, Szick Dániel, Tóth Adrián, Varga-Umbrich Eszter. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 8 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2015. novemberi fizika feladatai

