A P. 4783. feladat (2015. december)

P. 4783. \(\displaystyle \alpha=30^\circ\)-os hajlásszögű lejtőre helyezett \(\displaystyle m_1\) tömegű ék és annak vízszintes lapján lévő \(\displaystyle m_2\) tömegű kocka együtt gyorsulva mozog a lejtőn lefelé. Az ék és a lejtő között a súrlódási együttható 0,1.

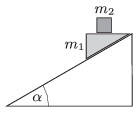
Legalább mekkora a súrlódási együttható a kocka és az ék között, ha a kocka nem csúszik meg az éken?

Közli: Szabó Miklós, Eger

(4 pont)

A beküldési határidő 2016. január 11-én LEJÁRT.

Megoldás. Az ék és a kocka egyetlen testként

\(\displaystyle a=g(\sin\alpha-\mu\cos\alpha)\)

gyorsulással csúszik le a lejtőn, ahol \(\displaystyle \alpha=30^\circ\) és \(\displaystyle \mu=0{,}1\). A kocka lejtő irányú (\(\displaystyle a \) nagyságú) gyorsulását az ék és a kocka közötti \(\displaystyle N\) nyomóerő, az \(\displaystyle m_2g \) gravitációs erő és valamekkora \(\displaystyle S\) nagyságú súrlódási erő biztosítja. A mozgásegyenletek:

\(\displaystyle m_2g-N=m_2a\cos\alpha,\)

\(\displaystyle S=m_2a\sin\alpha,\)

ahonnan

\(\displaystyle \frac{S}{N}=\frac{a\cos\alpha}{g-a\sin\alpha}=\frac{\tg\alpha-\mu}{1+\mu\tg\alpha}=0{,}45.\)

A kocka és az ék közötti súrlódási együtthatónak legalább ekkorának kell lennie, hiszen a kocka nem csúszik meg az éken. (Az eredmény független az \(\displaystyle m_1\) és \(\displaystyle m_2\) tömegektől.)

Statisztika:

99 dolgozat érkezett.
4 pontot kapott:	53 versenyző.
3 pontot kapott:	13 versenyző.
2 pontot kapott:	15 versenyző.
1 pontot kapott:	12 versenyző.
0 pontot kapott:	6 versenyző.

A KöMaL 2015. decemberi fizika feladatai