A P. 4786. feladat (2015. december)

P. 4786. Három pontszerű test - más testektől távol - úgy helyezkedik el a világűrben, hogy egy kezdeti pillanatban nem mozognak, és egymástól azonos $\displaystyle d$ távolságban vannak. Két test tömege egyenlő ($\displaystyle m$), a harmadik tömege $\displaystyle 2m$. A gravitációs vonzás hatására a testek mozgásba jönnek és egymásnak ütköznek.

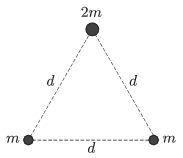
$\displaystyle a)$ Mekkora utat tesznek meg a testek a találkozásig?

$\displaystyle b)$ Mennyi idő telik el a testek ütközéséig?

(Lásd még ,,A gravitációs többtestprobléma két speciális esete'' című cikket Lapunk 558. oldalán.)

Nagy László fizikaverseny (Kazincbarcika) nyomán

(5 pont)

A beküldési határidő 2016. január 11-én LEJÁRT.

Megoldás. A mozgás során a testek egymástól mért távolsága mindvégig egyenlő nagyságú marad, tehát a három test pillanatnyi helyzete egy – egyre kisebb oldalélű – szabályos háromszöget jelöl ki. A találkozási pont a pontrendszer tömegközépppontja, ami mindvégig mozdulatlan marad (abban a vonatkoztatási rendszerben, amelyben a három test kezdetben nyugalomban volt), és a testek egyenes vonalú, változó gyorsulású mozgással haladnak a tömegközéppont felé.

$\displaystyle a)$ A tömegközéppont a $\displaystyle 2m$ tömegű testhez tartozó magasságvonal felezőpontja, ez a nehezebb testtől $\displaystyle s_1= \frac{\sqrt{3}}{4}d$, a 2 könnyebb testtől $\displaystyle s_{2,3}=\frac{\sqrt{7}}{4}d$ távolságra található, tehát ekkora utakat tesznek meg a testek a találkozásig.

$\displaystyle b)$ A testek összeütközéséig eltelő idő:

$\displaystyle T_0=\frac{\pi}{4}\sqrt{\frac{d^3}{2\gamma m}}.$

Ez az eredmény a hivatkozott cikk megfelelő képleteiből kapható meg, de úgy is levezethető, hogy Kepler III. törvényét alkalmazzuk a tömegközéppontba zuhanó testek elfajult ellipszispályáira.

Statisztika:

35 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Bartók Imre, Blum Balázs, Csenger Géza, Csuha Boglárka, Forrai Botond, Ghada Alshalan, Iván Balázs, Kasza Bence, Kovács Péter Tamás, Krasznai Anna, Németh 777 Róbert, Németh Flóra Boróka, Páhoki Tamás, Sal Kristóf, Szabó 199 Márton, Szentivánszki Soma , Tóth Adrián, Varga-Umbrich Eszter, Wiandt Péter.
4 pontot kapott:	Di Giovanni András, Jakus Balázs István, Juhász 326 Dániel, Olosz Adél, Szick Dániel, Szőke Dániel, Tomcsányi Gergely.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2015. decemberi fizika feladatai