 |
A P. 4804. feladat (2016. január) |
P. 4804. Vízszintes asztallapon egy \(\displaystyle m\) tömegű, homogén téglatestet húzunk az ábrán látható módon. A csigán átvetett zsineg egyik végét a téglatest felső (az ábra síkjára merőleges) oldalélének felezőpontjához rögzítettük, majd a másik végén ható \(\displaystyle F\) húzóerőt úgy változtatjuk, hogy a téglatest állandó sebességgel mozogjon. A test és az asztallap közötti csúszási súrlódási tényező \(\displaystyle \mu\).
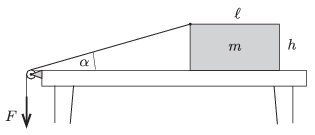
\(\displaystyle a)\) Adjuk meg, hogyan függ a zsinegben ható erő az ábrán látható \(\displaystyle \alpha\) szögtől!
\(\displaystyle b)\) Legfeljebb mekkora lehet az \(\displaystyle \alpha\) szög, mialatt a test a fenti módon, egyenletesen csúszva mozog?
Adatok: \(\displaystyle \ell=17{,}3\) cm, \(\displaystyle h=11\) cm, \(\displaystyle mg=10\) N, \(\displaystyle \mu=0{,}15\).
Közli: Légrádi Imre, Sopron
(6 pont)
A beküldési határidő 2016. február 10-én LEJÁRT.
Megoldás. Jelöljük a testre ható súrlódási erőt \(\displaystyle S\)-sel, az asztallap által kifejtett nyomóerőt pedig \(\displaystyle N\)-nel, a nyomóerő támadáspontjának (vízszintesen mért) távolsága a téglatest közepétől pedig legyen \(\displaystyle x\). (Nyilván fennáll, hogy \(\displaystyle x\le \ell/2\).)
A gyorsulásmentes mozgás feltétele:
\(\displaystyle F\cos\alpha-S=0,\)
\(\displaystyle F\sin\alpha+mg-N=0,\)
a csúszó súrlódás feltétele:
\(\displaystyle S=\mu N,\)
és végül a forgatónyomatékok egyensúlya (a tömegközéppontra vonatkoztatva):
\(\displaystyle \frac{h}{2}(F\cos\alpha+S)+\frac{\ell}{2} F\sin\alpha-xN=0.\)
\(\displaystyle a)\) Az egyenletrendszer megoldása:
\(\displaystyle F(\alpha)=\frac{\mu mg}{\cos\alpha-\mu\sin\alpha},\quad S(\alpha)=\frac{\mu mg\cos\alpha}{\cos\alpha-\mu\sin\alpha}, \quad N(\alpha)=\frac{mg\cos\alpha}{\cos\alpha-\mu\sin\alpha}.\)
\(\displaystyle b)\) A feladatban leírt mozgás biztosan nem jöhet létre, ha \(\displaystyle \tg\alpha\ge1/\mu\), vagyis \(\displaystyle \alpha\ge \alpha_1=81{,}4^\circ,\) hiszen ha a fokozatosan növekvő \(\displaystyle \alpha\) szög ehhez az értékhez közelít, az \(\displaystyle F\) erő (és vele együtt \(\displaystyle N\) és \(\displaystyle S\) is) minden határon túl növekszik; a zsineg tehát előbb-utóbb elszakad.
A téglatest egyenletes mozgása azonban már hamarabb is megszűnhet: ha a test felborul. Ez akkor következik be, amikor \(\displaystyle x\) eléri a kritikus \(\displaystyle \ell/2\) értéket. A forgatónyomatékra vonatkozó egyenlet szerint ez egy akkora \(\displaystyle \alpha_2\) szögnél következik be, amelyre
\(\displaystyle \tg\alpha_2=\frac1\mu-\frac{2h}{\ell}=5{,}4\approx 79{,}5^\circ.\)
Amikor \(\displaystyle \alpha\) eléri ezt a szöget, a test felborul.
Általában (a test méretarányaitól és tömegétől függetlenül) igaz, hogy \(\displaystyle \alpha_2<\alpha_1\), tehát \(\displaystyle \alpha\) növekedtével a test még a ,,megszorulása'' előtt felborul.
Statisztika:
66 dolgozat érkezett. 6 pontot kapott: Balogh Menyhért, Bekes Nándor, Csorba Benjámin, Csuha Boglárka, Elek Péter, Fajszi Bulcsú, Fehér 169 Szilveszter, Forrai Botond, Jakus Balázs István, Juhász 326 Dániel, Kasza Bence, Krasznai Anna, Mány Bence, Marozsák Tóbiás , Németh 777 Róbert, Németh Flóra Boróka, Olosz Adél, Sal Kristóf, Szabó Ágoston, Szőke Dániel, Tomcsányi Gergely, Tóth Adrián. 5 pontot kapott: Büki Máté, Kovács Péter Tamás, Simon Dániel Gábor. 4 pontot kapott: 29 versenyző. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2016. januári fizika feladatai

