 |
A P. 4812. feladat (2016. február) |
P. 4812. Egy gyűjtőlencse optikai tengelyén a lencsétől \(\displaystyle d\) távolságra egy \(\displaystyle T\) pontszerű fényforrás van. A lencse túlsó oldalán, az optikai tengelyre merőlegesen, a lencsével szemben egy síktükör van.
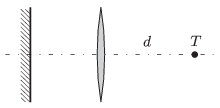
\(\displaystyle a)\) Ha a síktükröt az optikai tengely mentén mozgatjuk, akkor az optikai rendszer által a fényforrásról alkotott kép folyamatosan egybeesik a fényforrással. Hogyan lehetséges ez?
\(\displaystyle b)\) A fényforrás lencsétől mért távolságát megkétszerezzük. Hová helyezzük a síktükröt, hogy a rendszert elhagyó fénysugarak párhuzamosak legyenek egymással?
Közli: Zsigri Ferenc, Budapest
(4 pont)
A beküldési határidő 2016. március 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Ha a lencse fókusztávolsága \(\displaystyle f=d\), a lencsén áthaladó fénysugarak az optikai tengellyel párhuzamosak lesznek. Ugyanilyenek a tükörről visszaverődő fénysugarak is, melyek a lencsén ismételten áthaladva annak fókuszpontjában, vagyis a fényforrás helyén alkotnak képet.
\(\displaystyle b)\) A lencsétől \(\displaystyle x\) távolságban lévő tükör miatt az optikai rendszer úgy viselkedik, mint két egyforma, egymástól \(\displaystyle 2x\) távolságban lévő gyűjtőlencséből álló rendszer. Az első lencse a kétszeres fókusztávolságban lévő fényforrásról \(\displaystyle 2d\) távol alkot képet. Ha ez a képpont éppen a másik lencse fókuszpontja, akkor a továbbhaladó fénysugarak párhuzamosak lesznek egymással. Ennek feltétele: \(\displaystyle 2d+f=2x\), vagyis a lencse és a tükör távolsága \(\displaystyle x=\tfrac32\,d\).
Statisztika:
46 dolgozat érkezett. 4 pontot kapott: Asztalos Bogdán, Bartók Imre, Csire Roland, Csuha Boglárka, Debreczeni Tibor, Elek Péter, Gémes Antal, Horváth 914 Bálint, Kasza Bence, Kormányos Hanna Rebeka, Kovács Péter Tamás, Körmöczi Dávid, Krasznai Anna, Mándoki László, Marozsák Tóbiás , Molnár Mátyás, Nagy 555 Botond, Németh 777 Róbert, Németh Flóra Boróka, Páhoki Tamás, Pataki 245 Attila, Pázmán Előd, Póta Balázs, Pszota Máté, Radnai Bálint, Sal Kristóf, Sallai Krisztina, Simon Dániel Gábor, Szántó Benedek, Szepesi Zoltán, Szick Dániel, Tanner Martin, Tófalusi Ádám, Topa Lukács, Tóth 111 Máté , Tóth Bence, Török Péter, Varga-Umbrich Eszter, Veres Tamás, Wiandt Péter. 3 pontot kapott: Osváth Botond, Simon 727 Máté. 2 pontot kapott: 3 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2016. februári fizika feladatai
