A P. 4813. feladat (2016. február)

P. 4813. Tekintsük az ábrán látható hídkapcsolást!

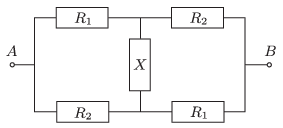
\(\displaystyle a)\) Mekkora a középső ellenállás értéke, ha az \(\displaystyle A\) és \(\displaystyle B\) pontok közötti eredő ellenállás éppen a középső ellenállás nagyságával egyezik meg: \(\displaystyle R_{AB}=X\)?

\(\displaystyle b)\) Megválasztható-e \(\displaystyle X\) értéke úgy, hogy az eredő ellenállás \(\displaystyle R_1\) és \(\displaystyle R_2\) négyzetes közepe legyen: \(\displaystyle R_{AB}=\sqrt{\dfrac{R_1^2+R_2^2}{2}}\)?

(Lásd még ,,A hídkapcsolás eredő ellenállása és áramerősségei'' című cikket Lapunk 105. oldalán, illetve ,,A Milne-egyenlőtlenség és társai, avagy ellenállások álruhában I.'' című cikket a KöMaL 2015. évi decemberi számának 514. oldalán.)

Közli: Bertalan Zoltán, Békéscsaba

(4 pont)

A beküldési határidő 2016. március 10-én LEJÁRT.

Megoldás. \(\displaystyle a)\) A hivatkozott első cikk (*) képlete szerint:

\(\displaystyle R_{AB}= \frac{X(R_1+R_2)+2R_1R_2}{R_1+R_2+2X} =X+2\frac{R_1R_2-X^2}{R_1+R_2+2X}.\)

A megadott feltétel akkor teljesül, ha \(\displaystyle X=\sqrt{R_1R_2},\) vagyis \(\displaystyle X\) a másik két ellenállás mértani közepével egyezik meg.

\(\displaystyle b)\) Az eredő ellenállás:

\(\displaystyle R_{AB}= \frac{X(R_1+R_2)+2R_1R_2}{R_1+R_2+2X},\)

ami \(\displaystyle X\)-nek monoton növekvő függvénye (ez a hivatkozott második cikkben Rayleigh monotonitási elveként szerepel). Ha \(\displaystyle X\) 0-tól végtelenig változik, akkor \(\displaystyle R_{AB}\) az \(\displaystyle R_1\) és \(\displaystyle R_2\) ellenállások harmonikus középétől a számtani közepéig terjedő értékeket vesz fel. Mivel az egymástól különböző pozitív számok négyzetes közepe nagyobb, mint a számtani közepük, nincs olyan \(\displaystyle X>0\) ellenállás, amelyre az eredő ellenállás \(\displaystyle R_1\) és \(\displaystyle R_2\) négyzetes közepével egyezne meg, ha azok különböző ellenállások. (Ha formálisan megoldjuk a megfelelő egyenletet, \(\displaystyle X\)-re negatív, fizikailag nem reális gyök adódik.) Természetesen \(\displaystyle R_1=R_2=R\) esetén \(\displaystyle R_{AB}=R\) a két egyforma ellenállás valamennyi középértékével (így a négyzetes közepükkel is) egyenlő.

Statisztika:

37 dolgozat érkezett.
4 pontot kapott:	Balogh Menyhért, Bekes Nándor, Csorba Benjámin, Csuha Boglárka, Di Giovanni András, Elek Péter, Fehér 169 Szilveszter, Iván Balázs, Körmöczi Dávid, Krasznai Anna, Marozsák Tóbiás , Molnár Mátyás, Nagy 555 Botond, Németh 777 Róbert, Németh Flóra Boróka, Olosz Adél, Paulovics Péter, Póta Balázs, Pszota Máté, Radnai Bálint, Sal Kristóf, Tomcsányi Gergely, Varga-Umbrich Eszter, Wiandt Péter.
3 pontot kapott:	Csenger Géza, Ghada Alshalan, Páhoki Tamás, Szűcs Győző.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2016. februári fizika feladatai