A P. 4875. feladat (2016. november)

P. 4875. Homogén anyagból készült félgömböt érdes, lapos lejtőre helyezünk, majd a lejtő hajlásszögét lassan növeljük.

\(\displaystyle a)\) Határozzuk meg a lejtő hajlásszögét abban az esetben, amikor a félgömb éppen megcsúszik a lejtőn, ha a tapadási súrlódási együttható értéke 0,3! Függ-e ez a hajlásszög attól, hogy a félgömböt sík felével vagy domború oldalával helyeztük a lejtőre?

\(\displaystyle b)\) Mekkora a lejtő és a félgömb sík oldala közötti szög a megcsúszás pillanatában akkor, ha a félgömböt domború oldalával helyeztük a lejtőre?

A továbbiakban tételezzük fel, hogy a lejtő és a félgömb közötti tapadási súrlódási együttható sokkal nagyobb a fenti értéknél. Kétféle kísérletet végzünk: egyszer a domború, másodszor pedig a sík felével helyezzük a félgömböt a lapos lejtőre. A lejtő hajlásszögét mindkét esetben lassan növeljük.

\(\displaystyle c)\) Legfeljebb mekkora lehet a lejtő hajlásszöge a két vizsgált esetben, hogy a félgömb a lejtőn nyugalomban maradhasson? Legalább mekkora tapadási súrlódási együttható szükséges a kritikus hajlásszög eléréséhez az egyik, illetve a másik esetben?

Közli: Honyek Gyula, Budapest

(5 pont)

A beküldési határidő 2016. december 12-én LEJÁRT.

Megoldás. Táblázati adatok szerint (lásd pl. a ,,Négyjegyű'' 198. oldalán az üreges félgömbre vonatkozó képletet) egy \(\displaystyle R\) sugarú homogén félgömb tömegközéppontja a geometriai középpontjától \(\displaystyle \tfrac38 R\) távolságban, a szimmetriatengelyén található.

\(\displaystyle a)\) A lejtőre helyezett – akármilyen alakú – merev test akkor csúszik meg, amikor a lejtő esésvonalával párhuzamos \(\displaystyle S\) súrlódási erő nagysága eléri a lejtőre merőleges \(\displaystyle N\) nyomórő \(\displaystyle \mu\)-szörösét, esetünkben 0,3-szorosát. Mivel az erőegyensúly feltételei miatt \(\displaystyle S=mg\sin\alpha\) és \(\displaystyle N=mg\cos\alpha\) (ahol \(\displaystyle \alpha\) a lejtő hajlásszöge, \(\displaystyle mg\) pedig a test súlya), a megcsúszás határszögére a \(\displaystyle \tg\alpha_0=0{,}3\) feltétel érvényes, ahonnan \(\displaystyle \alpha_0=16{,}7^\circ\). Ez az eredmény (amely csak a megcsúszás határhelyzetére vonatkozik) független attól, hogy melyik felével helyeztük a félgömböt a lejtőre. A továbbiakban vizsgálni kell még azt is, hogy vajon nem borul-e fel a test egy ilyen meredek lejtőn.

\(\displaystyle b)\) A domború oldalával lefelé álló félgömb csak akkor maradhat egyensúlyban a lejtőn, ha a \(\displaystyle C\) tömegközéppontja a lejtővel érintkező \(\displaystyle P\) pontja felett, azon átmenő függőleges egyenesen helyezkedik el. (Ellenkező esetben a súlyerőnek lenne az érintkezési pontra vonatkoztatott forgatónyomatéka, és emiatt a test elfordulna és felborulna). Ez a feltétel úgy valósulhat meg, hogy a félgömb síklapja a lejtő síkjához képest valamekkora \(\displaystyle \varphi\) szöggel elfordul.

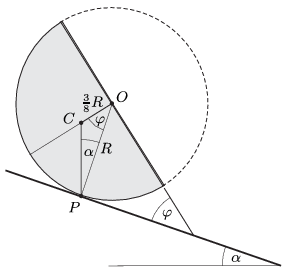
1. ábra

Az \(\displaystyle OPC\) háromszögre felírhatjuk a szinusztételt:

\(\displaystyle \frac{\sin\alpha}{\sin(\alpha+\varphi)}=\frac{3}{8},\)

ahonnan a megcsúszás \(\displaystyle \alpha=\alpha_0\) határszögénél (\(\displaystyle \mu=0{,}3\) esetén) a kérdéses szögre \(\displaystyle \varphi=33{,}3^\circ\) adódik.

\(\displaystyle c)\) Ha a tapadó súrlódási együttható az előzőnél nagyobb érték, akkor \(\displaystyle \alpha\) és vele együtt \(\displaystyle \varphi\) nagyobb is lehet, mint a fentebb kiszámított szög. De \(\displaystyle \alpha\) növelésével, ha

\(\displaystyle \sin\alpha>\frac{3}{8},\qquad \text{vagyis}\qquad \alpha>\alpha_1=22,0^\circ,\)

a szinusztételt kihasználó egyenletnek nincs megoldása \(\displaystyle \varphi\)-re, vagyis a félgömbnek nincs olyan egyensúlyi helyzete, amelynél a domború felével érintkezik a lejtővel; a félgömb tehát felborul. A határesetnek megfelelő szögnél a súrlódási együttható szükséges nagysága: \(\displaystyle \mu_1=\tg\alpha_1=0{,}40.\)

Amennyiben a félgömböt a sík felével helyezzük a lejtőre, majd növeljük a lejtő hajlásszögét, a félgömb ebből a helyzetéből is felborulhat, ha a tömegközéppontján átmenő függőleges egyenes a lejtővel érintkező körlapon kívülre kerül. A határesetnek megfelelő hajlásszög a \(\displaystyle \tg\alpha=\frac{8}{3}\) feltételből (2. ábra) \(\displaystyle \alpha=\alpha_2=69{,}4^\circ\) és a kritikus súrlódási együttható \(\displaystyle \mu_2=\tg\alpha_2=2{,}67.\)

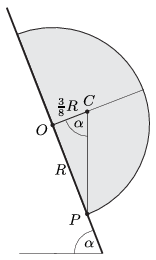
2. ábra

Az \(\displaystyle a)\) kérdésben szereplő \(\displaystyle \alpha_0\) szög kisebb, mint \(\displaystyle \alpha_1\) és \(\displaystyle \alpha_2\), tehát a félgömb sem a síklapjáról, sem pedig a domború oldaláról nem borulhat fel, mielőtt megcsúszna.

Statisztika:

40 dolgozat érkezett.
5 pontot kapott:	Bekes Nándor, Di Giovanni András, Mamuzsics Gergő Bence, Marozsák Tóbiás , Németh 777 Róbert, Tófalusi Ádám.
4 pontot kapott:	Fehér 169 Szilveszter, Jakus Balázs István, Mocskonyi Mirkó.
3 pontot kapott:	19 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2016. novemberi fizika feladatai