 |
A P. 4876. feladat (2016. november) |
P. 4876. Egy vízszintes tengelyű, rögzített cső bal oldali részének belső keresztmetszete \(\displaystyle A\), a jobb oldali résznek pedig \(\displaystyle kA\) a keresztmetszete, ahol \(\displaystyle k<1\) (pl. \(\displaystyle k=\frac{1}{5})\). A két rész az ábrán látható módon törésmentesen (,,simán'') csatlakozik egymáshoz. A csőben \(\displaystyle \varrho\) sűrűségű, elhanyagolható belső súrlódású folyadék van, amelynek a bal oldali csőrészben lévő részét egy dugattyú segítségével kinyomhatjuk onnan. A csövet elhagyó vízsugár egy, a cső tengelyére merőleges falnak csapódik, és azon – fokozatosan elvékonyodó folyadékhártyát képezve – szétterül.
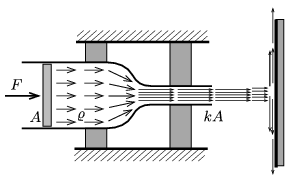
\(\displaystyle a)\) Mekkora állandósult sebességgel mozog a dugattyú, ha rá állandó, \(\displaystyle F\) nagyságú külső erő hat?
\(\displaystyle b)\) Mekkora erőt fejt ki a vízsugár a függőleges falra?
\(\displaystyle c)\) Mekkora vízszintes irányú erőt fejt ki a cső a rögzítésére?
Feltételezhetjük, hogy az áramlás időben állandó (stacionárius), és a gravitáció hatását a feladatban figyelmen kívül hagyhatjuk.
Közli: Sal Kristóf, UK, Cambridge
(6 pont)
A beküldési határidő 2016. december 12-én LEJÁRT.
Megoldás. A dugattyú viszonylag hamar (jó közelítéssel) egyenletesen fog mozogni. (Ez annál hamarabb következik be, minél kisebb \(\displaystyle k\) értéke. Ha \(\displaystyle k\rightarrow 1\), akkor nem alakul ki egyenletes mozgás, a dugattyú és a víz egyenletesen gyorsul.)
\(\displaystyle a)\) Jelöljük a dugattyú állandósult sebességét \(\displaystyle v\)-vel. A cső jobb oldali végénél kiáramló folyadék sebessége (a folyadék összenyomhatatlansága miatt) \(\displaystyle v/k\) lesz.
Tekintsük az áramló folyadékot valamelyik időpillanatban, illetve egy kicsiny \(\displaystyle \Delta t\) idővel később. A dugattyú elmozdulása ezalatt \(\displaystyle v\Delta t\), a külső erő munkája tehát
\(\displaystyle W=Fv\Delta t.\)
A csőből kiáramló folyadék tömege \(\displaystyle \Delta m=\varrho Av\Delta t\), sebessége \(\displaystyle v/A\), a teljes mozgási energia változása tehát
\(\displaystyle \Delta E=\frac{1}{2}\Delta m \left(\frac{v}{k}\right)^2-\frac{1}{2}\Delta m v^2.\)
(Úgy számolhatunk, mintha a dugattyú melletti \(\displaystyle \Delta m\) tömegű folyadékmennyiség \(\displaystyle v\) sebességről \(\displaystyle v/k\) sebességre gyorsult volna fel, és a folyadék többi részének sebessége nem változott volna.)
A munkatétel szerint \(\displaystyle W=\Delta E\), ahonnan
\(\displaystyle v=\sqrt{\frac{F}{\varrho A}\,\frac{2k^2}{1-k^2}}.\)
Ha például \(\displaystyle k=\tfrac{1}{5}\), akkor
\(\displaystyle v=\sqrt{\frac{F}{12\varrho A}}\approx 0{,}29\sqrt{\frac{F}{ \varrho A}}.\)
A dugattyú sebességét a
\(\displaystyle p+\varrho\frac{v^2}{2}+\varrho gh\)
Bernoulli-törvény felhasználásával is megkaphatjuk. A dugattyú közelében a folyadék nyomása \(\displaystyle p_0+\frac{F}{A}\), az áramlás sebessége pedig \(\displaystyle v\). A kiáramló folyadék nyomása a \(\displaystyle p_0\) külső légnyomással egyezik meg, sebessége pedig \(\displaystyle v/k\). A \(\displaystyle \varrho gh\) tag a gravitáció figyelmen kívül hagyása miatt nulla. Így
\(\displaystyle p_0+\frac{F}{A}+\frac{\varrho}{2}v^2=p_0+\frac{\varrho}{2} \,\frac{v^2}{k^2},\)
tehát
\(\displaystyle v=\sqrt{\frac{F}{\varrho A}\,\frac{2k^2}{1-k^2}}.\)
A munkatételből és a Bernoulli-törvényből kapott eredmény megegyezik, ami nem meglepő, hiszen a Bernoulli-törvény éppen a mechanikai energia megmaradását fejezi ki a folyadékok áramlásakor.
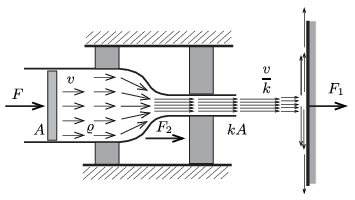
\(\displaystyle b)\) Ha a függőleges falnak csapódó víz \(\displaystyle F_1\) nagyságú, jobbra mutató erőt fejt ki a falra, akkor a fal ugyanekkora nagyságú, balra mutató erővel hat a folyadékra. Mivel \(\displaystyle \Delta t\) idő alatt \(\displaystyle \Delta m\) tömegű, \(\displaystyle v/k\) sebességű folyadék veszíti el vízszintes irányú lendületét, fennáll
\(\displaystyle -F_1\Delta t= -(\varrho A v \Delta t) \frac{v}{k},\)
vagyis (\(\displaystyle v\) korábban kiszámított értékét felhasználva)
\(\displaystyle F_1=\frac{2k}{1-k^2}\,F=\frac{5}{12}F\approx 0{,}42\, F. \)
\(\displaystyle c)\) A cső rögzítésére ható \(\displaystyle F_2\) erőt ugyancsak a lendületváltozás tételéből határozhatjuk meg. A folyadéknak a csőben lévő részére \(\displaystyle F-F_2\) erő hat, ezt a dugattyú, illetve a folyadéknyomásból származó, a szűkület falára ható erő ellenereje fejti ki. A lendületváltozás egyenlete:
\(\displaystyle \left(F-F_2\right)=\Delta m\left( \frac{v}{k}-v\right),\)
ahonnan
\(\displaystyle F_2=\frac{1-k}{1+k}\,F=\frac{2}{3}\,F\approx 0{,}67\,F.\)
Megjegyzés: Figyelemre méltó, hogy \(\displaystyle F_1+F_2\ne F\), de ez nem ellentmondás, hiszen (a sebességek időbeli állandósága ellenére) a teljes folyadékmennyiség lendülete időben egyre változik, csökken. Az eredő erő
\(\displaystyle F-F_1-F_2= -\frac{2k^2}{1-k^2}\,F\)
és ez éppen megegyezik a
\(\displaystyle \frac{\Delta I_\text{összes}}{\Delta t}= -\frac{\Delta m\cdot v }{\Delta t}=-\varrho A v^2\)
mennyiséggel, összhangban Newton II. törvényével.
Statisztika:
44 dolgozat érkezett. 6 pontot kapott: Bartók Imre, Bekes Nándor, Di Giovanni András, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Illés Gergely, Jakus Balázs István, Kavas Katalin, Marozsák Tóbiás , Nagy 555 Botond, Németh 777 Róbert, Olosz Adél, Páhoki Tamás, Sal Dávid, Szentivánszki Soma , Tófalusi Ádám. 5 pontot kapott: Elek Péter. 4 pontot kapott: 2 versenyző. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 11 versenyző.
A KöMaL 2016. novemberi fizika feladatai
