 |
A P. 4881. feladat (2016. november) |
P. 4881. \(\displaystyle N\) darab, \(\displaystyle 2f\) fókusztávolságú gyűjtőlencsét és \(\displaystyle N\) darab, \(\displaystyle -f\) fókusztávolságú szórólencsét helyezünk el egy optikai padon úgy, hogy a vékony lencsék felváltva, \(\displaystyle f\) távolságra kövessék egymást. A lencserendszerre az optikai tengellyel párhuzamos, \(\displaystyle D\) átmérőjű fénynyalábot bocsátunk
\(\displaystyle a)\) balról;
\(\displaystyle b)\) jobbról.
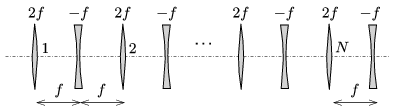
Milyen lesz a lencserendszert elhagyó fénynyaláb?
Amerikai példatári feladat
(4 pont)
A beküldési határidő 2016. december 12-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Az optikai tengellyel párhuzamosan balról érkező fénysugarakat a gyüjtólencse \(\displaystyle 2f\) távolságban fókuszálná, ha nem lenne ott a szórólencse. Ez a pont a szórólencse jobb oldali fókuszpontja, tehát az oda tartó sugarakat párhuzamossá teszi, de ennek a nyalábnak az átmérője már csak \(\displaystyle D/2\). A további lencsepárokon áthaladó fénnyel ugyanez történik, így a lencserendszert párhuzamos, \(\displaystyle D/2^N\) átmérőjű nyaláb hagyja el.
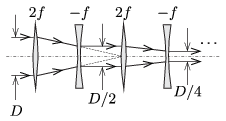
\(\displaystyle b)\) A jobbról érkező sugárnyalábbal hasonló történik, de a nyaláb mérete minden lencsepár után a 2-szeresére nő, így a végén \(\displaystyle 2^N\,D\) lesz. (Természetesen a nyaláb átmérőjének a lencsék mérete határt szab.)
Statisztika:
40 dolgozat érkezett. 4 pontot kapott: Berzsák Bulcsú, Bíró Dániel, Csuha Boglárka, Debreczeni Tibor, Elek Péter, Fehér 169 Szilveszter, Illés Gergely, Iván Balázs, Keltai Dóra, Kovács 124 Marcell, Krasznai Anna, Mácz Andrea, Makovsky Mihály, Markó Gábor, Marozsák Tóbiás , Mocskonyi Mirkó, Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Nyerges Dóra, Olosz Adél, Ónodi Gergely, Póta Balázs, Pszota Máté, Szentivánszki Soma , Tibay Álmos, Tófalusi Ádám, Turcsányi Ádám, Vajay Mónika, Varga-Umbrich Eszter, Zsók Bianka. 3 pontot kapott: Illyés András, Murányi Albert, Simon Ákos. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 5 versenyző.
A KöMaL 2016. novemberi fizika feladatai
